Алгоритмы текущей идентификации свойств объектов (Раздел 2.3 учебника "Планово-экономическое управление"), страница 3

Анализируя множество примеров, представленных в работах [23, 39, 54, 58, 64, 66], можно прийти к выводу, что наиболее целесообразным вариантом математической модели конкретной причинно- следственной связи в матрице пространства состояний, любой технической системы, является частотная модель вида:

,

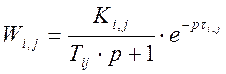
в которой лишь три параметра подлежат идентификации (коэффициент передачи, постоянная времени интегрирования и величина чистого запаздывания). Эта модель является аналогом линейного дифференциального однородного уравнения первого порядка, которое легко трансформировать в систему  m – ого порядка  по j-той причинно- следственной связи:

                 

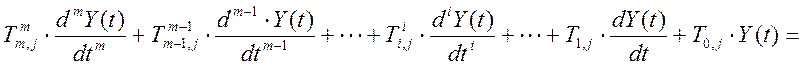
При этом, параметры этой математической модели легко идентифицируемы как по кривым разгона, так и корреляционным функциям сигналов. Эффективность идентификации полностью зависит от эффективности работы алгоритма текущей идентификации. Основным требованием к алгоритмам текущей идентификации является его работоспособность и эффективность в условиях нормальной эксплуатации системы управления. Это возможно только путем применения статистических  методов [34, 43, 44].

В основе рассматриваемого алгоритма текущей идентификации [10] лежит допущение о том,  что частные реализации основных технологических параметров нормального  функционирования производства представляют собой стационарные случайные эргодические процессы. Поэтому, вся  необходимая, для функционирования алгоритмов текущей идентификации, содержится   в    автокорреляционных и  взаимокорреляционных функциях входных и выходных параметров объекта управления:

                                ,                                                             

                                          .                                                              

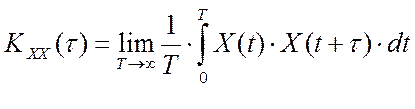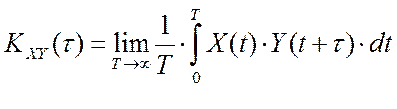где  X(t),  Y(t) – центрированные   значения   реализаций   входного    и         выходного     параметров  исследуемого объекта;  T – длина реализации по времени.

       Из кибернетической теории Роберта Винера  известно [10],  что  существует  связь   между  этими статистическими  характеристиками измеряемых сигналов и  импульсной  характеристикой  объекта исследования [20]:

                                      .                                    

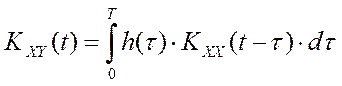В интеллектуальных измерительных системах, это уравнение может быть решаемо в реальном масштабе времени при условии синхронного вычисления корреляционных функции по текущим значениям входных и выходных параметрах объекта управления:

 

 ,  

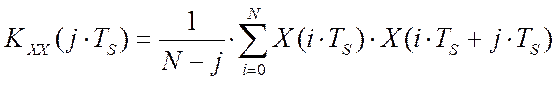
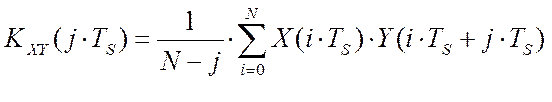где  X(iT_S), Y(iT_S)  – показания  соответствующих технических средств автоматизации, N  – длина массивов.

        Массив решетчатой автокорреляционной функции K_xx(jT_s) формируется в квадратную автокорреляционную матрицу, диагональные элементы которой  являются оценками дисперсии управляющего воздействия, K_xx(0):

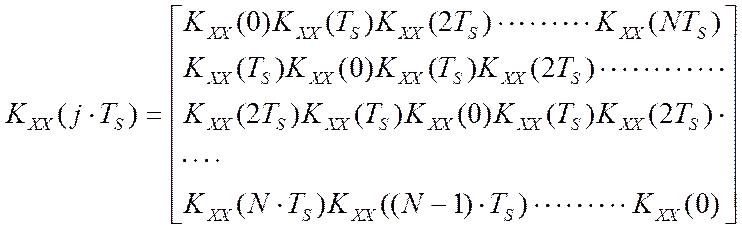
          Весовую же функцию  объекта управления можно  найти,  решив интегральное  уравнение 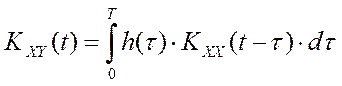 , решение которого  в  матричном  виде  имеет  вид:

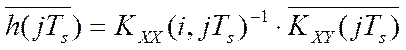                 .                            (2.33)                                        

Полученная  в  дискретных  значениях,  импульсная  переходная  характеристика объекта управления,  может  быть  использована в интеллектуальной измерительной системе для компенсации динамических свойств технической системы. Поскольку управляющие системы функционируют продолжительное время, то в составе информационных подсистем АСУТП необходимо иметь виртуальный прибор, который осуществляет текущую идентификацию динамических свойств объекта управления. Метрологические характеристики такого прибора могут быть также оценены по модели (2.31): 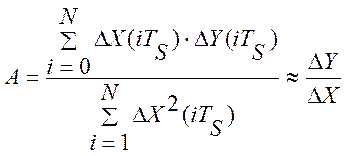, которая позволяет дать нам количественную оценку точности попадания в оптимум при управлении по градиентным алгоритмам управления. Эффективность алгоритма исследована в работе [27].  Из рисунка 2.21 видно, что дисперсия ошибки идентификации на всем диапазоне области определения управляющего воздействия лежит на прямой . Из рисунка 2.23 так же видно, что расчётное поле значений ошибок идентификации расположено вокруг статической характеристики объекта управления и определяет точность попадания в оптимум при управлении по градиентным и безмодельным алгоритмам управления. Как видно из рисунка 2.23, статическая методическая погрешность идентификации равна нулю. Это связано с процессами линеаризации и подчёркивает тот факт, что на погрешность идентификации большое влияние оказывает фиксация  положения  рабочей точки на протяжении всего периода идентификации.