Алгоритмы текущей идентификации свойств объектов (Раздел 2.3 учебника "Планово-экономическое управление"), страница 5

         Другое дело критерии оптимальности применяемые для реализации технических систем [1, 2, 4, 31, 32]. Уравнения измерения критериев оптимизации в этих технических системах представляют собой сложные нелинейные функции. Например, в работе [24] исследовались метрологические характеристики виртуального прибора для измерения количества выработанного тепла. Уравнение измерения имеет вид:                                       где Q(t) – это текущее значение количества тепла, Гкал, G₁₁(t) – текущее значение расхода теплоносителя,  T₁₂(t) – текущее значение температуры теплоносителя, c_p – изобарная теплоёмкость.  Из уравнения измерения виртуального прибора  видно, что измерительная система двух канальная и предназначена для обработки информации  об  одном потоке вещества. Или в работе [19], рассматриваются метрологические характеристики виртуального прибора по учёту количества потреблённого тепла. Уравнение измерения при этом имеет вид:                                     где Q(t) – это текущее значение количества потреблённого тепла, G₁₁(t) – текущее значение расхода прямого потока горячей воды, T₁₂(t) – текущее значение температуры прямого потока, c_p1 – теплоёмкость прямого потока, G₂₁(t) –  текущее значение расхода обратного потока горячей воды, T₂₂ (t) –  текущее значение температуры обратного потока, c_p2 – теплоёмкость обратного потока. Из уравнения измерения рассматриваемого виртуального прибора  видно, что измерительная система четырех канальная и предназначена для обработки информации о двух материальных   потоках.

           Ещё более сложными, с точки зрения проектировщиков и исследователей, являются интеллектуальные измерительные системы с дробным взаимодействием измерительных каналов. Например, в работах [4, 5,] исследован способ управления процессом абсорбции, который заключается в том, что изменяют расход абсорбента в зависимости от степени насыщения абсорбента. Степень насыщения при этом вычисляется измерительной системой по соотношению:

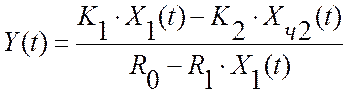
где X₁ (t) – концентрация абсорбента на выходе из абсорбера,  Xч2 (t) – концентрация абсорбента на входе в абсорбер,  К1,  К2, R0, R1 –  настроечные коэффициенты измерительной системы. В работе [62] виртуальный прибор, для этой цели,  реализует уравнение измерения, которое содержит динамические характеристики объекта управления как в числителе,  так и в знаменателе:

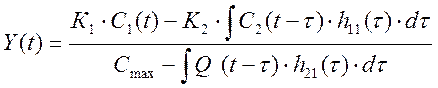
Здесь С₁(t), C₂(t)- соответственно, концентрации поглощаемого вещества в насыщенном и тощем абсорбенте, Q(t) – расход тощего абсорбента,  h₁₁ (t) – динамическая характеристика датчика измерения концентрации, h₂₁(t) – динамическая характеристика абсорбера по каналу управления, К1, К2, Cmax – настроечные коэффициенты виртуального прибора.

Эффективность работы парогазотурбинной электростанции целесообразно оценивать пятиканальной измерительной системой с уравнением измерения, предложенным в работе [64], где основными измеряемыми величинами выступают  W_г(t), W_п(t)- соответственно, текущие активные мощности газотурбинной и паротурбинной установок, Y_ij(t)- управляющие воздействия.  Работа по этому критерию позволяет держать максимальной текущую эффективность работы электростанции,  , при меньших расходах газа.  

       Таким образом, уравнения измерения текущих значений критерия управления являются нелинейными функциями текущих показаний технических средств автоматизации и хотя бы по этому требуют линеаризации перед применением в системах адаптивного управления. В работах [24, 51, 56, 58, 64] показано, что наиболее эффективным методом линеаризации при проектировании робастных систем является разложение функции в ряд Тейлора.  

Рассмотрим, в качестве примера, уравнение измерения выходного сигнала  измерительной системы состоящей из N измерительных каналов и соединённых в единую измерительную систему с помощью уравнения измерения: Y(t)=Y₁(t)Y₂(t)...Y_N(t).   Здесь Y₁(t), Y₂(t), ..., Y_N(t) – некоторые входные  параметры, с которыми функционально связан результат измерения Y(t). Исследование такой системы усложняется тем, что операция, связывающая значения параметров  Y_i(t) с выходным значением всей измерительной системы нелинейная.     В теории случайных процессов, существует теорема о сумме статистических независимых случайных величин, подчиненных нормальному закону распределения [34]. Согласно этой теореме указанная сумма представляет собой также нормальную случайную величину. Совместная плотность вероятности двух коррелированных нормальных случайных величин, средние значения которых отличны от нуля, равна: