Алгоритмы текущей идентификации свойств объектов (Раздел 2.3 учебника "Планово-экономическое управление"), страница 4

                На рисунке 2.24 представлен график зависимости дисперсии ошибки идентификации от периода опроса датчиков, T_S , [27] Из рисунка видно, что дисперсия ошибки имеет минимум при периоде опроса датчиков T_S=10 секунд, который можно трактовать как оптимальную настройку идентификатора, который реализует решение интегрального уравнения: 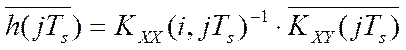 (см. 2.33 и работу [27]).

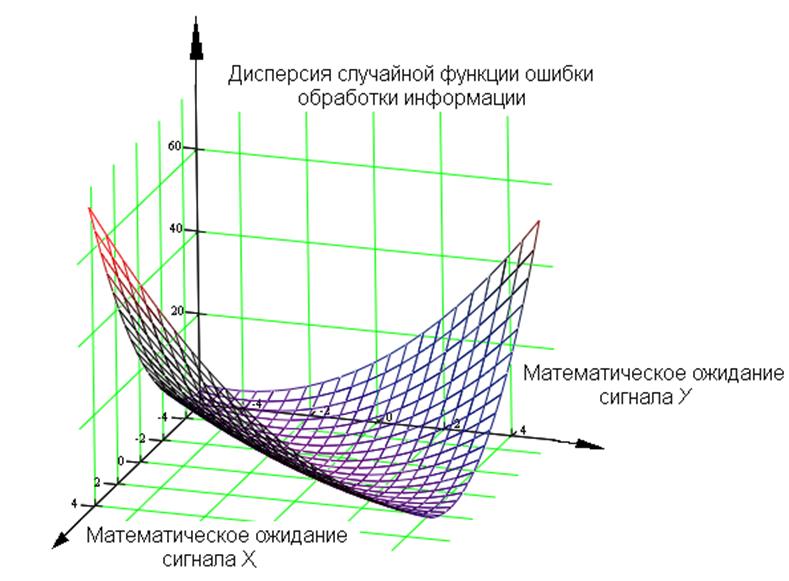
Рис. 2.23– Ошибки текущей идентификации в точке линеаризации

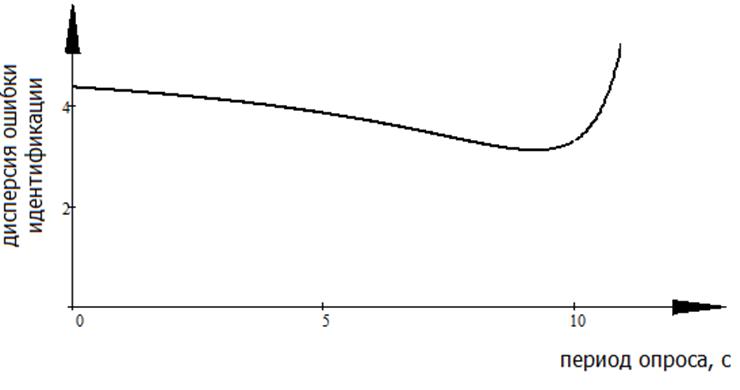
Рис. 2.24 Ошибки идентификации от скважности решетчатых функций

2.4    Критерии эффективности функционирования технической системы

Сложность современных управляющих систем во многом зависит от уравнения измерения, которое определяет количество измерительных каналов, участвующих в формировании информации для расчета текущего значения критерия управления. Уравнение измерения также определяет и сложность математической модели формирования методической динамической составляющей погрешности измерения критерия управления. Таким образом, сложность всех алгоритмов измерения, алгоритмов визуализации процессов измерения и алгоритмов оптимального управления зависит от сложности уравнения измерения критерия оптимальности. Как было представлено выше, в общем случае уравнение измерения текущего значения критерия оптимальности в реальном масштабе времени имеет вид [54 и (2.11)]:

                                                                                                        

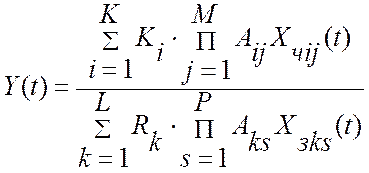
где K - количество аддитивных каналов измерения в числителе критерия управления, L-  количество аддитивных каналов измерения в знаменателе критерия управления, M- количество мультипликативных  каналов измерения в числителе критерия управления, P- количество мультипликативных каналов измерения в знаменателе критерия управления, К_i и R_k - настроечные коэффициенты информационно-измерительной подсистемы.  Из записи обобщенного критерия следует, что в общем виде уравнение измерения критерия управления является нелинейной функцией большого числа переменных. Среди этих переменных есть константы, которые играют роль настроечных коэффициентов различных устройств (узлов) технической системы. А некоторые параметры технической системы представляют собой случайные функции времени. В некоторых случаях критерием оптимизации является линейный обобщенный технологический или технико-экономический параметр (например, перепад температур, текущая себестоимость производства). Уравнение измерения, в этом случае, принимает вид: 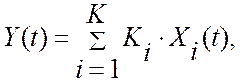  где K  – число измерительных каналов. Основной особенностью таких многоканальных измерительных систем является смешанная обработка входных и выходных координат объекта управления и, если объект управления динамический, то входные переменные критерия оптимизации должны быть приведены к выходным. А само уравнение измерения критерия оптимальности, при этом, принимает вид интегрального соотношения:

                                                         

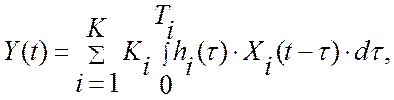
Здесь  h_i(t)- импульсная динамическая характеристика технической системы по рассматриваемому каналу управления. Например, при управлении процессом каталитического разложения диметилдиоксана в производстве синтетического каучука широко используется принцип управления реактором по перепаду температур [3, 5]. Поскольку процесс идет с выделением тепла, то в канале измерения входной температуры должен стоять компенсатор динамических свойств реактора. Уравнение измерения виртуального прибора для измерения перепада температур будет иметь вид:            

                        

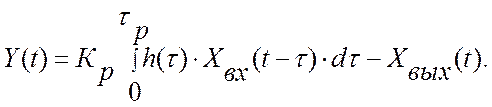
Здесь Y(t) – текущее значение перепада температур, Хвх(t) – текущее значение температуры на входе в реактор, Хвых(t) – текущее значение температуры на выходе из реактора, h(τ) – динамическая характеристика реактора, К_р - коэффициент передачи, τ_р – длина импульсной характеристики реактора.  Только при выполнении этих ограничений обе температуры и перепад будут считаться измеренными в один момент времени, t. Естественно, что критерии управления в приведённых примерах не требуют линеаризации, так как в их структуре нет нелинейных операций.