4.2.3 Диагностика потерь текущей идентификации
При адаптивном
управлении критерием качества, чаще всего, выбирается технологический
коэффициент полезного действия (текущая эффективность) Y(iTS) [54]. Текущая эффективность как
критерий качества робастной системы определяется как отношение текущего
значения критерия управления, измеряемого виртуальным прибором, ![]() , к текущему значению критерия управления,
прогнозируемому по эталонной математической модели объекта управления,
, к текущему значению критерия управления,
прогнозируемому по эталонной математической модели объекта управления, ![]() :
: 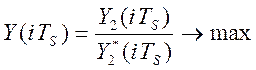 . Априорно
известно, что этот критерий имеет максимум, дрейфующий в пространстве
управляющих координат. Текущее положение экстремума рассчитать невозможно, так
как дрейф критерия управления является нестационарным случайным процессом и,
как правило, характеристики этого случайного процесса неизвестны. Однако можно
количественно, с помощью метода наименьших квадратов, оценить статистическую
оценку знака и величины градиента этого критерия. По знаку градиента можно
принимать решение о направлении изменения управляющих координат при случайных
перемещениях статической характеристики в пространстве управляющих координат.
Составляющие вектора градиента могут являться рекомендациями по изменению
управляющих воздействий при адаптивном управлении и, позволяют следить за
перемещениями статической характеристики объекта управления в пространстве
управляющих координат. Показания виртуальных
приборов, Y(iTS), зависят от свойств алгоритмов идентификации динамических свойств объекта управления. При этом
особенно актуальными становятся вопросы настройки этих алгоритмов и некоторых
элементов измерительного канала. Требуется постоянная корректировка, как
динамических свойств объекта управления, так и динамических свойств элементов
измерительной системы. Как правило, вся
необходимая, для функционирования алгоритмов текущей идентификации,
содержится в текущих значениях решётчатой автокорреляционной функции
управляющего воздействия:
. Априорно
известно, что этот критерий имеет максимум, дрейфующий в пространстве
управляющих координат. Текущее положение экстремума рассчитать невозможно, так
как дрейф критерия управления является нестационарным случайным процессом и,
как правило, характеристики этого случайного процесса неизвестны. Однако можно
количественно, с помощью метода наименьших квадратов, оценить статистическую
оценку знака и величины градиента этого критерия. По знаку градиента можно
принимать решение о направлении изменения управляющих координат при случайных
перемещениях статической характеристики в пространстве управляющих координат.
Составляющие вектора градиента могут являться рекомендациями по изменению
управляющих воздействий при адаптивном управлении и, позволяют следить за
перемещениями статической характеристики объекта управления в пространстве
управляющих координат. Показания виртуальных
приборов, Y(iTS), зависят от свойств алгоритмов идентификации динамических свойств объекта управления. При этом
особенно актуальными становятся вопросы настройки этих алгоритмов и некоторых
элементов измерительного канала. Требуется постоянная корректировка, как
динамических свойств объекта управления, так и динамических свойств элементов
измерительной системы. Как правило, вся
необходимая, для функционирования алгоритмов текущей идентификации,
содержится в текущих значениях решётчатой автокорреляционной функции
управляющего воздействия: 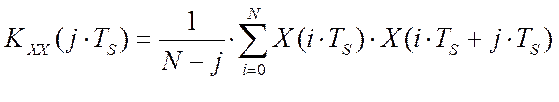 и текущих
значениях взаимокорреляционной функции управляющего воздействия и критерия
управления:
и текущих
значениях взаимокорреляционной функции управляющего воздействия и критерия
управления: 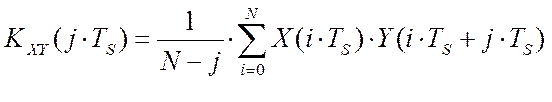 , где X(iTS), Y(iTS)–показаний
соответствующих приборов, N – длина
массива.
, где X(iTS), Y(iTS)–показаний
соответствующих приборов, N – длина
массива.
Из теории автоматического управления известно [10], что существует связь между этими статистическими характеристиками измеряемых сигналов и импульсной характеристикой объекта управления:
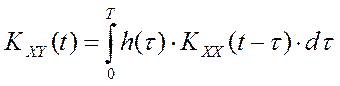 .
.
Весовую функцию объекта управления можно идентифицировать, включив в состав системы управления дополнительный модуль УСО [27], который предназначен для решения этого интегрального уравнения в матричном виде:
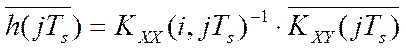 . (4.28)
. (4.28)
При решении этого уравнения требуются значительные вычислительные мощности. Это связано как с формированием массивов корреляционных функций, так и с особенностями формирования квадратной корреляционной матрицы, элементы которой являются показаниями виртуального прибора для измерения текущих значений критерия управления:
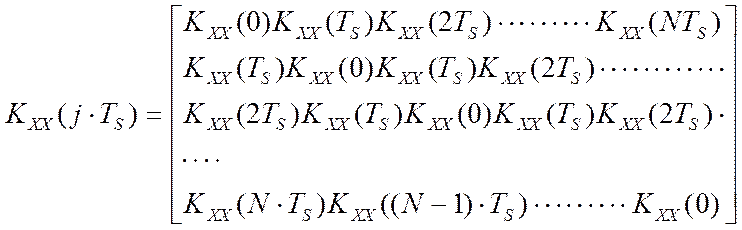
Применение, в составе информационных подсистем АСУТП, таких типовых модулей связи с объектом управления, которые осуществляют не только измерение текущих значений параметров технологического процесса и вычисление текущих значений критерия управления, но и проводят текущую идентификацию динамических свойств объекта управления (полевой изменяемый прибор [27] в дальнейшем, идентификатор).
Основной метрологической характеристикой идентификатора, конечно же должна являться ошибка идентификации динамической модели объекта управления, так как идентифицируемая весовая функция объекта управления входит в уравнение измерения и все ошибки идентификации переносятся через уравнение измерения на метрологические характеристики показаний виртуального прибора. Систематические ошибки при идентификации носят как инструментальный характер, так и методический. Причём, если на инструментальные составляющие погрешности повлиять нельзя (поскольку они заложены технологией изготовления прибора), то методические составляющие погрешности можно существенно снизить за счёт оптимальной настройки программного обеспечения полевого изменяемого прибора. При этом, настройками программного обеспечения являются скважность корреляционных функций (период опроса датчиков), TS , и длина массивов корреляционных функций, N . При этом, основные ошибки возникают из-за процесса дискретизации по времени, ТS , и нелинейного вида уравнений для вычисления корреляционных функций. После линеаризации путем разложения в ряд Тейлора в окрестности математического ожидания множества реализаций управляющего воздействия М{ХJ(iTs)} для автокорреляционной функции и сохранения в разложении лишь членов первого порядка, имеем [27]:
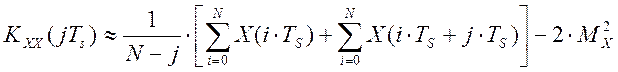 . (4.29)
. (4.29)
Линеаризация уравнения для вычисления взаимокорреляционной функции, проведенная путем разложения уравнения измерения в ряд Тейлора в окрестности математических ожиданий множества реализаций стационарного случайного процесса ХJ(iTs) и нестационарного случайного процесса YJ(iTs) , с сохранением в разложении лишь членов первого порядка, дает следующее линеаризованное уравнение для вычисления взаимокорреляционной функции:
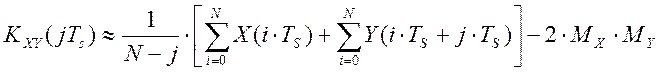 (4.30)
(4.30)
Текущее значение ошибки идентификации может быть определено как разность между показаниями аналогового (эталонного) вычислителя выражения (4.30), KXY(iTS) , и показаниями полевого изменяемого прибора Z(iTS) [30]: E(iTS) = KXY(iTS) – Z(iTS).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.