Диагностика потерь текущей идентификации (Раздел 4.2.3 учебника "Планово-экономическое управление"), страница 2

         Для типовой структуры интеллектуального измерительного канала вычислителя относительная методическая динамическая погрешность идентификации взаимокорреляционной функции в условиях действия высокочастотной некоррелированной помехи будет иметь следующую модель [64]:

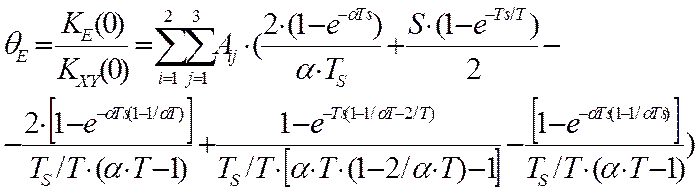 ,        (4.31)       

где S- уровень по­мехи; α - скорость изменения измеряемых сигналов, K_XY(0) – оценка взаимокорреляционной  функции в нуле,  K_XX(0)  - оценка автокорреляционной функции в нуле. Матрица коэффициентов линеаризации, при этом, имеет вид:

                               .

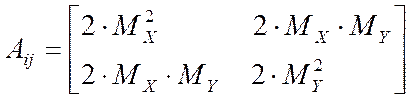Модель относительной методической динамической ошибки идентификации взаимокорреляционной функции, в условиях действия коррелированной помехи,  будет иметь  вид [64]:

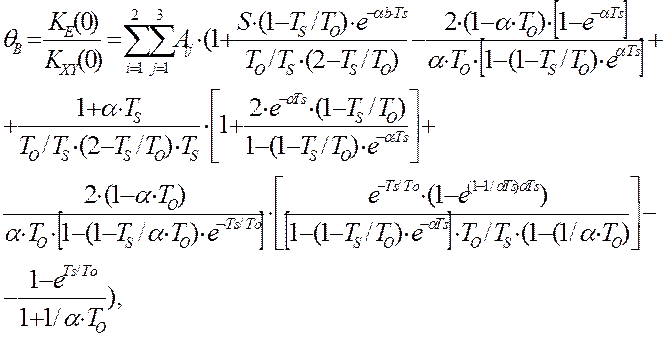           (4.32)

где T_S - период опроса датчика; Т_O - постоянная времени объекта управления; S - уровень помехи; b-  скорость изменения выходной координаты объекта управления; α - скорость изменения входной координаты объекта управления, K_XY(0) – оценка взаимокорреляционной функции в нуле.

Когда параметры объекта управления измеряются инерционными датчиками (плотномеры, хроматографы, кондуктометры и т.п.). Тогда, математическая модель относительной методической динамической  ошибки идентификации взаимокорреляционной  функции принимает вид [64]:

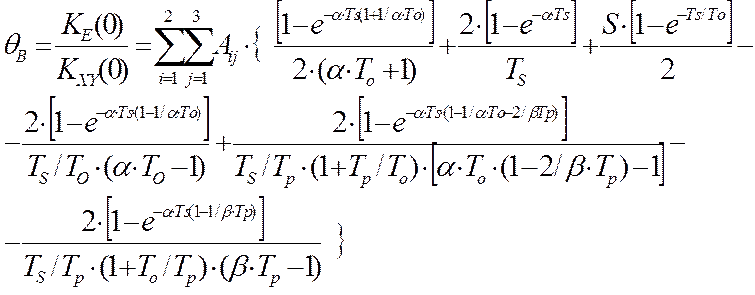         (4.33)

            Модели погрешностей (4.31 -:- 4.33) показывают, что ошибка идентификации – это регулируемая величина. Она  меняется при  изменении периода опроса датчиков (T_S). Кроме того, на погрешность идентификации большое влияние оказывает длина массива. Причем, длина массивов должна быть не менее 100 измерений, что вполне согласуется с теорией вероятности и классической формулой для количественной оценки потерь информации принятой в теории связи  GИ = S/(m-2), где S – это уровень помехи, а m – это количество некоррелированных измерений. Обычно, за интервал некоррелированности принимают три  постоянных времени автокорреляционной функции обрабатываемого сигнала, а на интервале времени равному постоянной времени автокорреляционной функции должно быть не менее десяти измерений.

              Модели метрологических характеристик (4.31 -:- 4.33)  ориентированы на устройство, которое отвечает основным требованиям, предъявляемым к виртуальному прибору: автоматический опрос входного и выходного параметров объекта управления; периодический расчет корреляционных функции и их визуализация; решение интегрального уравнения (4.28).  Результаты математического моделирования процессов измерения и процессов формирования относительной методической динамической погрешности обработки измерительной информации по модели (4.33) (см. рис.4.9) показывают, что методическая динамическая составляющая погрешности цифровой обработки измерительной информации имеет экстремальный вид. Оптимальный режим функционирования идентификатора достигается при  αT_S =14, а уровень относительной погрешности, при этом составляет 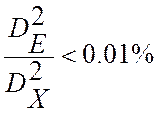 . В работе [27] проводилась идентификации весовой функции эндогазогенератора по каналу управления расход газа – влажность эндогаза. А методическая динамическая составляющая погрешности идентификации, рассчитанная по модели (4.33) дает нам количественную оценку потерь информации при управлении по градиентным алгоритмам управления.

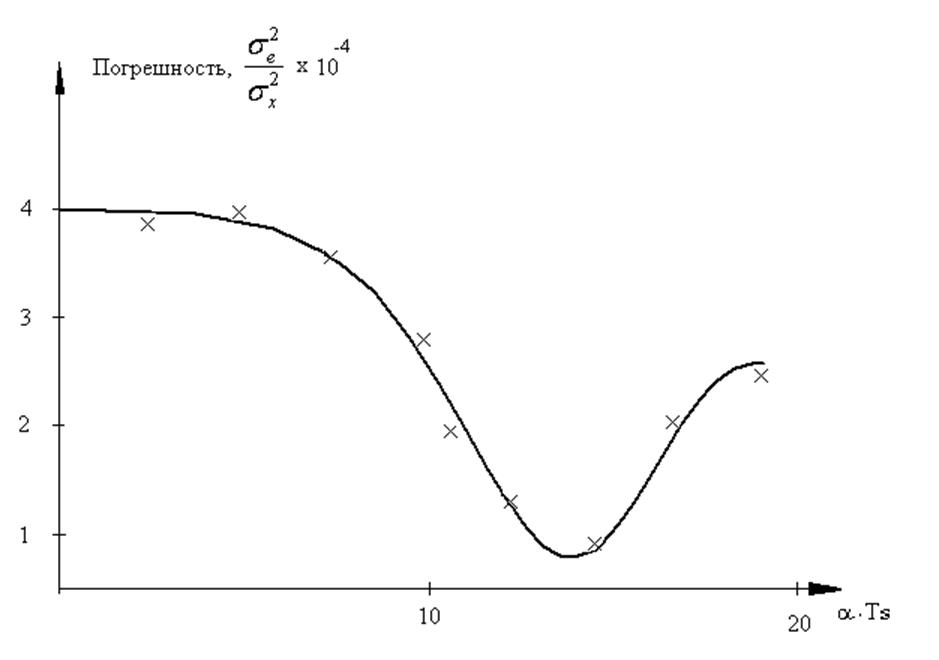
Рис. 4.9  Погрешность идентификации текущих значений

               взаимокорреляционной функции

 Проверка адекватности модели (4.33) проводилась методом математического моделирования с применением критериев Фишера и Стьюдента. На рисунке 4.9 сплошной линией представлены расчёты по модели (4.33), а крестиками представлены результаты имитационного моделирования.