Диагностика потерь текущей идентификации (Раздел 4.2.3 учебника "Планово-экономическое управление"), страница 3

       На рисунке 4.10 представлено поле ошибок идентификации взаимокорреляционной функции, из которого видно, что расчётное поле значений ошибок идентификации расположено вокруг статической характеристики технической системы и определяет удалённость рабочей точки   от экстремума при управлении по градиентным и безмодельным алгоритмам управления.

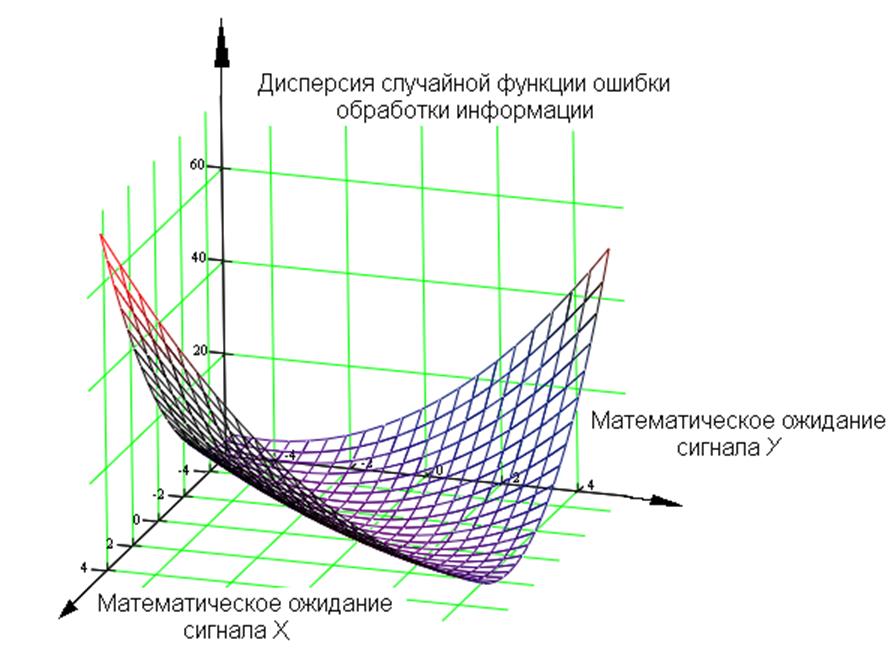
Рис. 4.10  Поле ошибок  идентификации K_XY(iT_S)

        Кроме того, (см. рис. 4.10) статическая методическая погрешность идентификации равна нулю. Это связано с процессами линеаризации и подчёркивает тот факт, что на погрешность идентификации большое влияние оказывает фиксация  положения  рабочей точки на протяжении всего периода идентификации.

            Метрологические свойства идентификатора [27], как виртуального прибора, оцениваются тремя основными метрологическими характеристиками.  Для количественной оценки дисперсии показаний идентификатора можно использовать математическую модель (4.34), которая получена для случая измерения коррелированных сигналов [64], каковыми и являются входные и выходные координаты динамического объекта управления:          

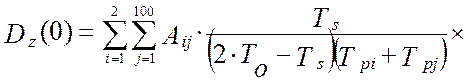
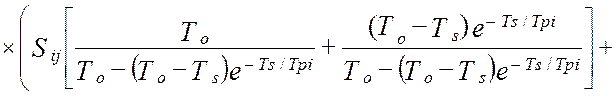
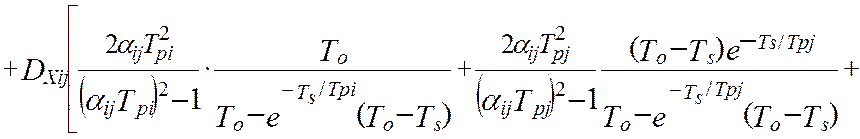
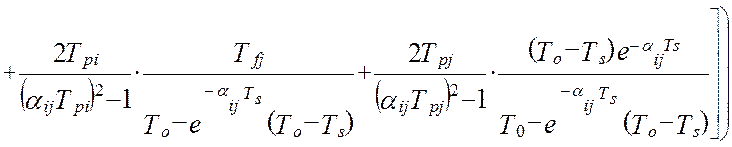.         (4.34)

При этом взаимокорреляционная функция показаний эталонного вычислителя и показаний идентификатора будет иметь вид [64]

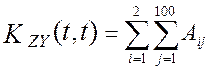
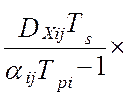
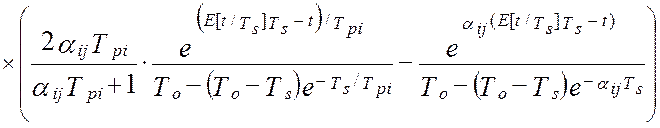,                   (4.35)

а, дисперсия ошибок идентификации взаимокорреляционной функции будет равна [64]:

 

               

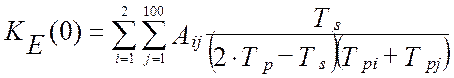
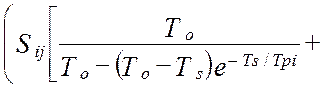
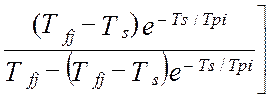
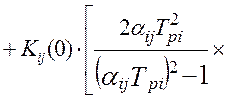
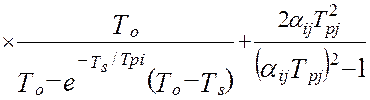
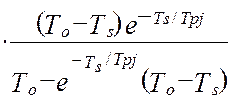
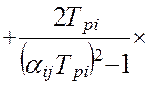
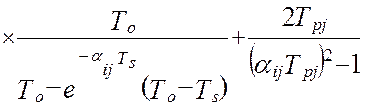
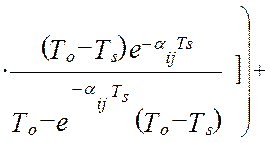
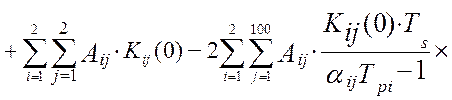
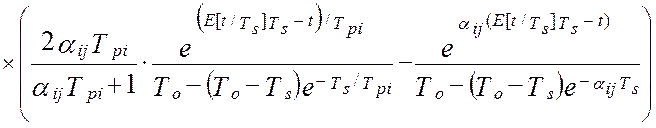.                    (4.36)

В моделях (4.34 -:- 4.36): A_ij– это матрица коэффициентов линеаризации;  T_S – единый период дискретизации всех функций времени; T_o – постоянная времени объекта управления; T_pi– постоянные времени динамических характеристик эталонных преобразователей; α_ij– диагональная матрица скоростей изменения измеряемых величин;  E[t/T_S] – дискретное время (операция взятия целой части числа); S_ij– диагональная матрица уровней помех измерения; K_ij(0) – корреляционная матрица измеряемых сигналов при t=0 (диагональные элементы – это дисперсии измеряемых сигналов, все остальные элементы матрицы – это значения взаимокорреляционной функции показаний эталонной измерительной системы и идентификатора).

        Таким образом, модели (4.31 -:- 4.36) – это основные метрологические характеристики программного обеспечения прибора предназначенного для идентификации корреляционных функций и динамических свойств объекта управления.  Прибор состоит из первичного преобразователя (полевой изменяемый прибор [27]), который производит опрос входных и выходных координат объекта управления, расчет корреляционных функций и их визуализацию. Оператор анализирует внешний вид корреляционных функций и принимает решение о наличии взаимосвязи координат. Если взаимосвязь обнаружена, то проводится текущая идентификация динамических свойств объекта управления.

          Проверка работоспособности прибора и адекватности математических моделей метрологических характеристик проводилась на стенде для диагностики программного обеспечения виртуальных приборов, созданного специально для этих целей [29], по методикам из работы [23].  Информационно-измерительные каналы стенда (см. рисунок 4.11)  реализуют чистую передачу измерительной информации, которая имитируется в автоматизированном рабочем месте (см. гл. 4.4). Поэтому метрологические характеристики эталонного вычислителя и  идентификатора полностью определяются элементами стенда, эталонной моделью объекта управления и режимами цифровой обработки информации. При моделировании измерительной системы, статическая характеристика  датчиков измерительной информации принималась линейной с коэффициентом передачи равным единица, то есть Y(t) =X(t). Динамические свойства датчика измерительной информации принимались  в виде апериодического звена первого 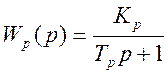порядка , где K_p – коэффициент передачи, T_p–  время. Для процесса формирования дисперсии погрешности идентификации эталонного переходного процесса, как решения однородного линейного дифференциального уравнения первого порядка 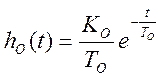  , который может быть представлен в виде решётчатой функции: 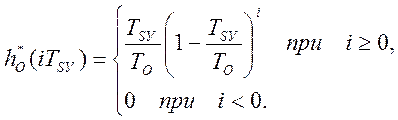, где Т_SУ – скважность решётчатой функции идентификатора, Т_O   и K_O – параметры эталонной модели объекта управления.