СИСТЕМЫ ИСЧИСЛЕНИЯ.
Предметом изучения курса "Цифровые устройства" являются импульсные устройства, формирующие и преобразующие стандартные импульсные сигналы. Стандартными называют сигналы, для которых фиксированы значения верхнего и нижнего уровней. Если верхний уровень принимается за уровень единицы, а нижний за уровень нуля, то говорят, что цифровое устройство использует положительную (прямую) логику.
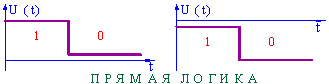
Положительная логика может быть реализована как в области положительных напряжений, так и в области отрицательных.
Если нижний уровень импульсного сигнала принять за единицу, а верхний – за ноль, то такая логика называется негативной или инверсной.
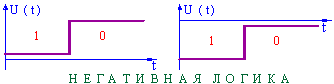
Она также может быть реализована как в области положительных напряжений, так и в области отрицательных.
Поскольку в цифровых устройствах напряжение принимает только два возможных уровня, то все изменения этих напряжений удобно представлять числами в двоичной (бинарной) системе исчисления. Двоичная система исчисления относится к классу позиционных систем исчисления, которых существует бесконечное множество. Под системой исчисления понимают способ представления любого числа с помощью символов, называемых цифрами. Позиционной называется система исчисления, в которой значение одной и той же цифры различно и зависит от позиции, занимаемой цифрой в последовательности цифр, изображающих число. Наиболее распространенной позиционной системой исчисления является десятичная, в которой используются десять цифр от нуля до девяти. В общем случае число в позиционной системе исчисления представляется по следующему правилу:
![]() ,
,
где S – основание системы исчисления (в десятичной – 10, в
двоичной – 2), а – цифры, используемые в этой системе исчисления. Т.о. число в
условной записи записывается следующим образом: ![]() .
Запятая разделяет целую и дробную части числа. Как видим, вес каждой цифры
зависит от ее позиции. В двоичной системе исчисления вес каждого разряда,
определяется, как целочисленная степень двойки, т.е. а –2 – ¼, а –1
– ½, а0 – 1, а1 – 2, а2 – 4, а3 – 8, и т.д.
.
Запятая разделяет целую и дробную части числа. Как видим, вес каждой цифры
зависит от ее позиции. В двоичной системе исчисления вес каждого разряда,
определяется, как целочисленная степень двойки, т.е. а –2 – ¼, а –1
– ½, а0 – 1, а1 – 2, а2 – 4, а3 – 8, и т.д.
При необходимости ввода в цифровое устройство оператором каких-либо чисел, представленных в двоичной системе, запись числа (особенно большого) превращается в длинную последовательность единиц и нулей, что часто приводит к ошибкам. Для сокращения записи желательно использовать такие системы исчисления, которые позволяли бы:
1. резко сократить количество цифр записи числа;
2. преобразование цифр из этой системы исчисления в двоичную и обратно
должно быть простым.
Примером такой системы исчисления может служить восьмеричная система исчисления, у которой используются цифры от 0 до 7, а основание S=8. при этом любая из цифр этой системы исчисления представляется трехразрядным (трех битовым) двоичным числом:
![]() .
.
В этом случае, восьмеричная форма записи выглядит следующим образом:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.