Цифровые устройства как учебная дисциплина, страница 7

В приведенном примере самой большой склейкой является склейка из восьми клеток (склейка ).

  II.  Одна и та же клетка может участвовать в нескольких склейках. Это имеет

смысл в том случае, если удается тем самым увеличить размер склейки.

 III.  В процессе формирования склеек необходимо стремиться к образованию

склеек максимально возможного размера.

IV.  Количество склеек должно быть минимальным, однако, склейками должны

быть охвачены все единицы, имеющиеся в карте.

Каждая из склеек формирует слагаемое минимизированной функции. Получается это слагаемое следующим образом. В пределах склейки определяются те логические переменные, которые не меняют своего значения. Т.о., в рассматриваемом примере, первая склейка дает слагаемое "b" , вторая склейка –  и третья – . В результате получаем минимизированную форму записи исходной функции в следующем виде:

.

Из полученного в примере результата видно, что чем крупнее склейка, тем меньше сомножителей в соответствующем слагаемом. Если какая-либо клетка не входит ни в одну из склеек, т.е. при k=0, то слагаемое, находящееся в этой клетке, переписывается без изменений.

Рассмотрим еще один пример. Предположим, что исходная логическая функция имеет следующий вид:

.

Заполняем карту Карно.

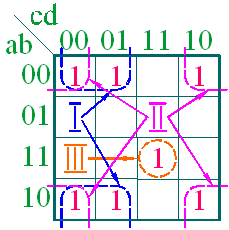В данном случае можно провести три склейки, следовательно, минимизированная функция будет содержать три слагаемых:

.

Существует класс логических функций, которые называются недоопределенными. Недоопределенные функции это такие логические функции, для которых существуют запрещенные комбинации входных переменных, т.е. такие логические комбинации, которые не могут появиться на входе ни при каких обстоятельствах.

Например, при преобразовании двоичного кода в десятичный. Для представления десятичных цифр в двоичном коде необходимо четыре разряда. Поэтому при заполнении таблицы истинности, соответствующей такому преобразованию, таблица будет содержать шестнадцать строк, из которых будут использоваться только первые десять. Остальные шесть строк использоваться не будут, т.е. при схемной реализации такого преобразователя эти шесть входных комбинаций никогда не появятся на входе. Т.о. эти последние шесть комбинаций для такого преобразования являются запрещенными.

При минимизации недоопределенных логических функций необходимо учитывать эти запрещенные состояния, поскольку это позволяет дополнительно упростить минимизированную функцию.

Предположим, что в рассмотренном выше примере существует три запрещенных состояния: .

Внесем эти запрещенные состояния в карту Карно.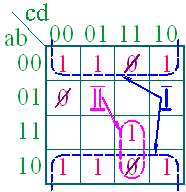

При минимизации клетки с запрещенными состояниями проектировщик вправе по своему усмотрению принимать как за ноль, так и за единицу. При этом, единственным критерием выбора является увеличение размеров склеек и уменьшение их числа.

В рассматриваемом примере эту задачу можно решить, если два запрещенных состояния принять за единицу, а одно – за ноль, как показано на приведенном рисунке. Тогда, при организации склеек, получаем одну склейку из восьми клеток и одну склейку из двух. И минимизация исходной логической функции, с учетом запрещенных состояний, приводит к следующему результату:

.

Т.о. одна и та же исходная логическая функция при минимизации может быть существенно упрощена, если учитывать запрещенные состояния.