Цифровые устройства как учебная дисциплина, страница 6

Карта Карно представляет собой прямоугольную таблицу, количество клеток в которой равно 2ⁿ, где n – число логических переменных минимизируемой логической функции.

 Минимизация с помощью карт Карно наглядна при количестве логических переменных меньше или равно 4. Если n>4, то ситуация несколько усложняется и минимизацию проводят, как правило, при помощи компьютеров.

Рассмотрим процесс минимизации, полагая n=4, т.е. для y(a, b, c, d). Карта Карно для четырех переменных состоит из 16 клеток. По строкам будем менять значение переменных a и b, а по столбцам с и d.

Для минимизации логической функции y(a, b, c, d), прежде всего, необходимо представить её в СДНФ.

Рассмотрим в качестве примера минимизацию следующей логической функции: .

1.  Приведем данную логическую функцию к нормальной форме, т.е.

преобразуем исходное выражение к следующему виду:

.

Т.о., используя правило де'Моргана и раскрывая скобки в последнем слагаемом, мы избавились от отрицания над несколькими переменными, и пришли к ДНФ.

2.  Далее, приведем, полученную в предыдущем пункте, ДНФ к совершенной

форме. Для этого используем правило  для тех слагаемых, в которых отсутствуют какие-либо переменные. Поскольку , то очевидно, что умножение xy на 1 не меняет значения логической функции.

Итак,

.

.

В результате проведенных преобразований исходная логическая функция будет представлена в СДНФ:

 .

После приведения подобных, получаем:

.

3.  Поскольку заданная логическая функция представлена

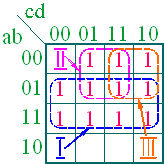
теперь в СДНФ, то можно заполнить карту Карно:

Для этого в клетки карты, соответствующие слагаемым, представленной для минимизации, функции, записываются единицы.

4.  Особо следует остановиться на процессе организации

склеек.

Значения переменных в соседних клетках карты, как по строкам, так и по столбцам, отличаются значением только одной переменной (так организована карта). Кроме того, крайние клетки в строках и столбцах, так же, отличаются значением только одной переменной и называются соседними. Такая организация карты необходима для того, чтобы организовать закон склейки – . Т.о. если взять две единицы в соседних клетках и склеить их по меняющейся переменной, то получим одно слагаемое минимизированной логической функции в виде произведения переменных, не меняющих свое значение в пределах этих двух клеток.

Склейкой называется объединение 2^k клеток, где k=0, 1, 2, …, n, где n – количество входных переменных.

При организации склеек необходимо исходить из следующих правил:

  I.  Форма склейки может быть только прямоугольной, причем в одну склейку,

как уже было указано, может входить лишь количество клеток равное 2^k. Кроме того, единицы, расположенные в крайних или угловых клетках, могут склеиваться по строкам и (или) по столбцам с единицами, расположенными в соседних (т.е. находящихся с другой стороны карты) клетках, если таковые имеются.