Цифровые устройства как учебная дисциплина, страница 4

ПРЕОБРАЗОВАНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ.

Мы уже отмечали, что любая, сколь угодно сложная функция может быть представлена с помощью операций (И), (ИЛИ), (НЕ). Но, как правило, эта логическая функция не всегда представлена в простейшем виде. Преобразование (упрощение) логических функций производят, пользуясь правилами алгебры логики. Эти законы можно разбить на несколько групп:

1.  Законы одинарных элементов. а+1=1, а+0= а, а ^.1= а, а ^. 0=0.

2.  Комбинационные законы.

3.  Переместительный и сочетательный законы.

.

. .

.

4.  Дистрибутивный (распределительный) закон.

5.  .

6.  Закон поглощения. .

7.  Закон склейки. .

8.  Закон Де–Моргана. .

Закон Де–Моргана очень полезен при необходимости преобразовании ненормальной формы записи в нормальную. В тоже время этот закон наглядно показывает дуальность алгебры логики, смысл которой в следующем: если возникает необходимость замены логической операции (И) на операцию (ИЛИ) или наоборот, то достаточно проинвертировать каждую переменную в отдельности и результат в целом.

Пользуясь этими законами можно осуществлять минимизацию логических функций.

МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ.

Существует несколько методов минимизации (упрощения) формул логических функций. Сама процедура минимизации проводится с целью получения простейшей записи, при аппаратурной реализации которой полученная схема отличалась бы минимальным количеством логических элементов, а, следовательно, и стоимостью. Общих методов, позволяющих с помощью стандартных приемов получить простейшую запись формул, не существует. Разработаны несколько методов, которые позволяют это делать при наличии определенных навыков. Одним из возможных методов является метод, который заключается в последовательном преобразовании логических функций, пользуясь правилами алгебры логики (чаще всего правилами поглощения и склейки).

Пример: минимизировать следующую логическую функцию: .

Для минимизации этой функции необходимо применить правило, которое является общим для всех методов минимизации, правило Де–Моргана, поскольку имеется общее отрицание над несколькими переменными. Т.о. получаем следующее выражение:

.

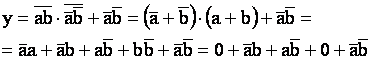Согласно комбинационному закону , к полученному результату можно прибавить , без изменения общего значения функции. Тогда:

.

Полученная запись может быть преобразована далее, согласно закону склейки:

.

Если бы к первоначальному результату не было дописано дополнительное слагаемое , то решение имело бы следующий вид:

.

Далее, согласно дистрибутивному закону, получаем следующий результат:

.

Использование такого приема, однако, может, иногда, приводить к тупиковым формулам, которые логически эквивалентны исходным выражениям, однако, переход от одного к другому невозможен. Простейшая форма записи любой логической функции, в частности, является тупиковой формулой. Например: