Чисельний пошук екстремуму функції однієї змінної. Чисельні методи пошуку екстремуму функції декількох змінних

 Глава 9

 Чисельний пошук екстремуму функції однієї змінної

Більшість задач оптимізації зводиться до пошуку найбіль-шого (або найменшого) значення деякої функції. Методи матема-тичного аналізу зручні для вирішення цієї проблеми, коли функ-ція задається явно і є при цьому диференційованою. Коли ж функція задається табличним способом або аналітично громіздкою формулою, ефективними є чисельні методи розв’язку.

Функція однієї змінної  називається унімодальною на відрізку , якщо на ньому знаходиться єдина точка , в якій функція набуває мінімального значення.

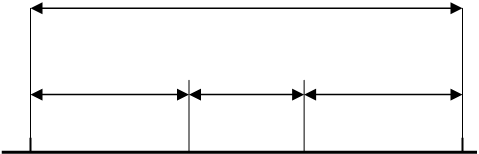
9.1 Метод золотого перетину

Золотим перетином відрізка  називається розподіл його точкою  на дві нерівні частини так, щоб відношення усього відрізка до більшої частини дорівнювало відношенню більшої частини до меншої

                                  1,6180339

            0,6180334       0,381966       0,6180334

       a                        c                 d                         b

                                 Рисунок 9.1

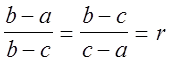.                                  (9.1)

Число  називають золотим  відношенням. Його значення відоме: 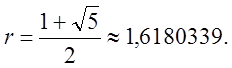 На відрізку  можна визначити дві симетрично розміщені точки  і , що реалізують золотий перетин. Їх знаходимо за формулами

,

.

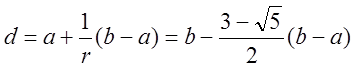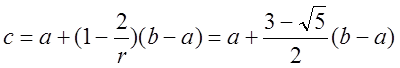Опишемо алгоритм мінімізації функції однієї змінної , вважаючи її унімодальною на відрізку . Початковий відрізок  ділимо точками  (перша точка) і  (друга точка) за прави-лом золотого перетину і у цих точках обчислюємо значення функ-цій  і . Порівняння цих значень дозволяє відкинути або інтервал , якщо , або інтервал , якщо . Довжина  відрізка , що залишився , зменшиться у  разів:

.

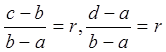Після цього процес повторюємо.

На  інтервалі , що залишився , уже є одна точка , що робить його золотий перетин :  є друга точка золотого перетину відрізка ,а  -перша точка золотого перетину відрізка . Знаючи одну з точок золотого перетину , іншу можна знайти за однією із вищезгаданих формул та обчислити значення  у знову знай-деній точці (значення в іншій точці вже обчислено на попередньо-му кроці).

Таким чином,на кожному кроці ,починаючи з другого, потрібно лише одне обчислення функції , і інтервал невизна-ченості зменшується в  разів:

Точка мінімуму

Після  кроків маємо довжину інтервала невизначеності:

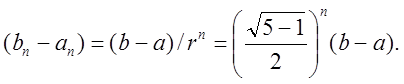                     (9.2)

Процес золотого перетину продовжуємо доти ,поки інтер-вал  стане менше деякого заданого числа , названого точністю.

           З формули випливає ,що при  довжина відрізка, який залишився , прагне до нуля як геометрична прогресія зі зна-менником  ,тобто метод золотого перетину завжди збігається, причому лінійно. Число кроків , що забезпечують задану точ-ність  знаходження точки мінімуму ,повинно задовольняти нерівність:

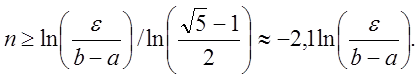                (9.3)

Використовуючи цю формулу , можна знайти необхідне чи-сло кроків  для забезпечення необхідної точності .Однак на практиці часто роблять інакше: визначають межу відрізка  за формулою (9.2) і потім порівнюють із заданою точністю .

Метод золотого перетину гарантує знаходження мінімуму в самих несприятливих умовах ,коли функція є не тільки недиферен-ційованою ,але і навіть має розриви першого роду .

Алгоритм мінімізації функції методом золотого перетину

1  Знаходимо точки і  за формулами

  де

2  Обчислюємо значення функції  та  і порівнюємо їх:

a)  якщо  то за інтервал невизначеності беремо відрізок  і знаходимо його золотий перетин , приймаючи    , та обчислюємо

b)  якщо  за інтервал невизначеності беремо відрізок  і знаходимо його золотий перетин, вважаючи

   , та обчислюємо

3  Перевіряємо умову . Якщо ця нерівність виконуєть-ся, то за точку мінімуму приймаємо величину 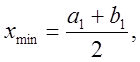 якщо ні, то повертаємося до пункту 1.

4  Процес повторюємо доти, поки для деякого  не справдиться .

Приклад. Знайти мінімум функції  на відрізку  з точністю  

Розв’язок. Функція  є унімодальною на , тому що  для

            Користуючись вищевказаним алгоритмом, знаходимо інтервал , що містить точку екстремуму. Обчислення розмістимо в таблиці.

Таблиця 9.1

Потрібна точність досягається при

  .

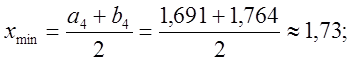
Завдання 10 1 Показати ,що функція f(x) унімодальна .

2 Знайти мінімальне значення функції f(x) і точку мінімуму  на відрізку  з точністю .

  1  f(x)=(х+2)/x²-x,                              [-1;-0,5].

  2  f(x)=x+1/ln(x),                               [1,5;2,5].

  3  f(x)=x+ln²(x),                                    [0,3;1].

  4  f(x)=x-ln(ln(x)),                               [1,3;2,3].

  5  f(x)=x+1/arctg(x),                           [0,5;1,5].