Міністерство освіти і науки України
Сумський державний університет
Звіт
до лабораторної роботи №6
з предмету «Чисельні методи»
на тему
«Інтерполяційний многочлен Лагранжа. Сплайни.»
Варіант № 9
Підготував:
Студент групи ІН-71
Конопленко А.В.
Перевірила:
Назаренко Л.Д.
Суми 2009
1. Умова задачі
Завдання 6 Для функції y=f(x), що задана таблично, побудувати інтерполяційний многочлен і сплайн. Обчислити в заданій точці x* значення функції і встановити, якою з інтерполюючих функцій доцільніше скористатися.
|
Номер вар. |
Значення |
x* |
|
9 |
x 0 1 2 3 4 |
2,5 |
|
y 2 6 14 38 90 |
2. Обґрунтування алгоритму.
2.1 Інтерполяційний многочлен Лагранжа
Інтерполяційний многочлен Лагранжа, що набуває у вузлах інтерполяції 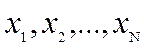 відповідно значень
відповідно значень 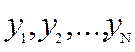 має
вигляд
має
вигляд
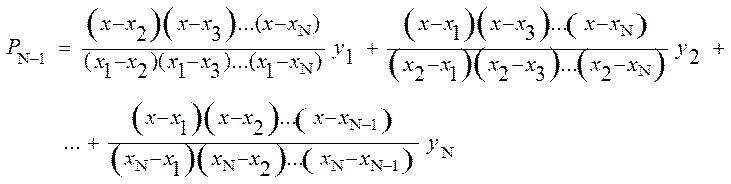
2.2 Сплайни.
Кубічний сплайн є найкращою з функцій, що інтерполюють задану функцію.
Отже, якщо 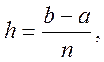
![]() (
(![]() ),
), ![]() , то
кубічний сплайн на цьому відрізку
, то
кубічний сплайн на цьому відрізку
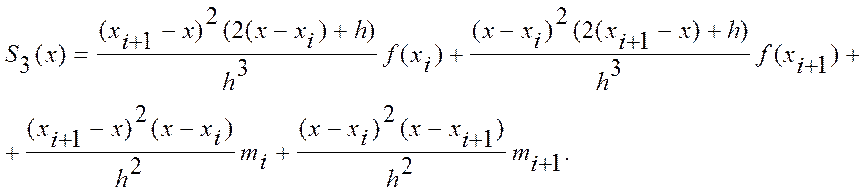
Тут 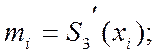
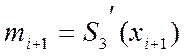 .
.
Якщо відомо
![]() , то відповідна система
рівнянь
, то відповідна система
рівнянь
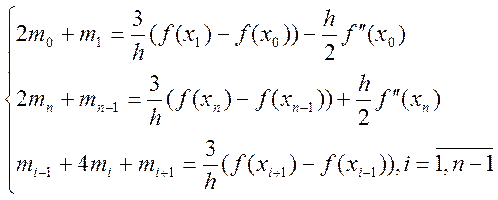 (5.29)
(5.29)
Якщо є можливість вибору між граничними (крайовими) умовами 1-го та 2-го типу, то перевагу слід надати умовам 1-го типу.
У випадку, коли ніякої додаткової інформації про поведінку
апроксимованої функції нема, часто використовують так звані природні
граничні (крайові) умови ![]() .
.
3. текст програми.
program spline_legrange;
uses wincrt;
const eps=0.0001;
n=5;
h=1;
type mas=array[1..n]of real;
var m,m1,b,d,summ,x,y:mas;
i,j,l:integer;
norm,Mm,Delta,x0,splin,s1,s2,z:real;
A,C:array[1..n,1..n]of real;
procedure lagrange(y,x:mas;x0:real;var z:real);
var i,j:integer;
g,f:real;
begin
for i:=1 to 5 do
begin
f:=1;
g:=1;
for j:=1 to 5 do
begin
if (i<>j) then
begin
f:=f*(x0-x[j]);
g:=g*(x[i]-x[j]);
end;
end;
z:=z+f*y[i]/g;
end;
end;
function zeidel1(x:mas):real;
begin
zeidel1:=C[1,2]*x[2]+C[1,3]*x[3]+C[1,4]*x[4]+C[1,5]*x[5]+D[1]
end;
function zeidel2(x:mas):real;
begin
zeidel2:=C[2,1]*x[1]+C[2,3]*x[3]+C[2,4]*x[4]+C[2,5]*x[5]+D[2]
end;
function zeidel3(x:mas):real;
begin
zeidel3:=C[3,1]*x[1]+C[3,2]*x[2]+C[3,4]*x[4]+C[3,5]*x[5]+D[3]
end;
function zeidel4(x:mas):real;
begin
zeidel4:=C[4,1]*x[1]+C[4,2]*x[2]+C[4,3]*x[3]+C[4,5]*x[5]+D[4]
end;
function zeidel5(x:mas):real;
begin
zeidel5:=C[5,1]*x[1]+C[5,2]*x[2]+C[5,3]*x[3]+C[5,4]*x[4]+D[5]
end;
{max norma}
function max(x,x1:mas):real;
var s:real;
begin s:=abs(x[1]-x1[1]);
for i:=2 to 5 do if abs(x[i]-x1[i])>s then s:=abs(x[i]-x1[i]);
max:=s;
end;
{--------}
begin
writeln(' vvedite to4ky:');
write('x=');
readln(x0);
x[1]:=0; x[2]:=1; x[3]:=2; x[4]:=3; x[5]:=4;
y[1]:=2;y[2]:=6;y[3]:=14;y[4]:=38;y[5]:=90;
a[1,1]:=2; a[1,2]:=1; for i:=3 to n do a[1,i]:=0;
a[2,1]:=1; a[2,2]:=4; a[2,3]:=1; a[2,4]:=0; a[2,5]:=0;
a[3,1]:=0; a[3,2]:=1; a[3,3]:=4; a[3,4]:=1; a[3,5]:=0;
a[4,1]:=0; a[4,2]:=0; a[4,3]:=1; a[4,4]:=4; a[4,5]:=1;
for i:=1 to 3 do a[5,i]:=0; a[5,4]:=1; a[5,5]:=2;
b[1]:=9; b[2]:=42; b[3]:=108; b[4]:=210; b[5]:=135;
for i:=1 to n do
for j:=1 to n do
begin
if (i=j) then c[i,j]:=0
else c[i,j]:=-a[i,j]/a[i,i];
end;
for i:=1 to n do
d[i]:=b[i]/a[i,i];
Mm:=0;
for i:=1 to n do
begin
if (abs(C[i,1])+abs(C[i,2])+abs(c[i,3])+abs(c[i,4]))>Mm
then Mm:=abs(c[i,1])+abs(c[i,2])+abs(c[i,3])+abs(c[i,4]);
end;
norm:=Mm;
Delta:=(1-norm)*eps/norm;
for i:=1 to n do
m[i]:=1;
repeat
for i:=1 to n do
begin
m1[i]:=m[i];
end;
m[1]:=zeidel1(m);
m[2]:=zeidel2(m);
m[3]:=zeidel3(m);
m[4]:=zeidel4(m);
m[5]:=zeidel5(m);
until max(m,m1)<delta;
for i:=1 to 4 do
if ((x0>x[i])or(x0=x[i])) and ((x0<x[i+1])or(x0=x[i+1])) then l:=i;
s1:=(sqr(x[l+1]-x0)*(2*(x0-x[l])+h)*y[l]+sqr(x0-x[l])*(2*(x[l+1]-x0)+h)*y[l+1])/h*h*h;
s2:=(sqr(x[l+1]-x0)*(x0-x[l])*m[l]+sqr(x0-x[l])*(x0-x[l+1])*m[l+1])/h*h;
splin:=s1+s2;
writeln(' spline:');
writeln('S(x)=',splin:1:4);
lagrange(y,x,x0,z);
writeln(' polinom Lagranga:');
writeln('L(x)=',z:2:4);
end.
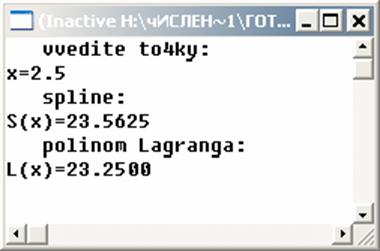
Реалізація в Maple:
ПоліномЛагранжа:
> restart;
with(LinearAlgebra):
x:=array(1..5):
y:=array(1..5):
x0:=2.5;
L:=0:
x[1]:=0: x[2]:=1: x[3]:=2: x[4]:=3: x[5]:=4:
y[1]:=2: y[2]:=6: y[3]:=14: y[4]:=38: y[5]:=90:
for i from 1 by 1 to 5 do
b:=1:
a:=1:
for j from 1 by 1 to 5 do
if (i<>j) then a:=a*(x0-x[j]):
b:=b*(x[i]-x[j]):
end if:
end do:
L:=L+a*y[i]/b:
end do:
lagrange;
L;
![]()
![]()
![]()
сплайн:
> restart;
s:={2*m1+m2=9,m1+4*m2+m3=42,m2+4*m3+m4=108,m3+4*m4+m5=210,m4+2*m5=135}:
R := solve( s ):
m:=array(1..5):
x:=array(1..5):
y:=array(1..5):
m[1]:=3/2: m[2]:=6: m[3]:=33/2: m[4]:=36: m[5]:=99/2:
x[1]:=0: x[2]:=1: x[3]:=2: x[4]:=3: x[5]:=4:
y[1]:=2: y[2]:=6: y[3]:=14: y[4]:=38: y[5]:=90:
x0:=2.5;
h:=1:
for i from 1 by 1 to 4 do
if ((x0>x[i])or(x0=x[i])) and ((x0<x[i+1])or(x0=x[i+1])) then l:=i: end if:
spl:=((x[l+1]-x0)^2*(2*(x0-x[l])+h)*y[l]+(x0-x[l])^2*(2*(x[l+1]-x0)+h)*y[l+1])/h*h*h+((x[l+1]-x0)^2*(x0-x[l])*m[l]+(x0-x[l])^2*(x0-x[l+1])*m[l+1])/h*h:
end do:
spline;
spl;
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.