§ 7. Абсолютная величина и норма матрицы
Неравенство
![]() (1)
(1)
Между
матрицами 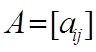 и
и ![]() одинаковых
типов обозначает, что
одинаковых
типов обозначает, что
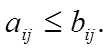 (2)
(2)
В этом смысле не всякие две матрицы сравнимы между собой.
Под
абсолютной величиной (модулем) матрицы ![]() будем
понимать матрицу
будем
понимать матрицу
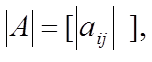
где
![]() – модули элементов матрицы
– модули элементов матрицы ![]() .
.
Если
![]() и
и ![]() –
матрицы, для которых операции
–
матрицы, для которых операции ![]() и
и ![]() имеют смысл, то:
имеют смысл, то:
а) ![]()
б) 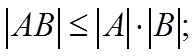
в) 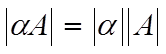
( ![]() - число).
- число).
В частности, получаем:
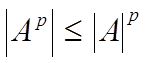
(
![]() - натуральное число).
- натуральное число).
Под нормой матрицы ![]() понимается действительное число
понимается действительное число ![]() , удовлетворяющее условиям:
, удовлетворяющее условиям:
а) ![]() причем
причем
![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() =0;
=0;
б) 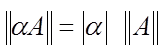 (
(
![]() - число ) и, в частности,
- число ) и, в частности, ![]() ;
;
в) 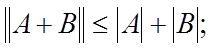
г) 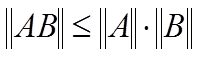
(![]() и
и ![]() - матрицы, для которых соответствующие
операции имеют смысл). В частности, для квадратной матрицы имеем:
- матрицы, для которых соответствующие
операции имеют смысл). В частности, для квадратной матрицы имеем:
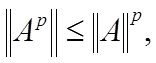
где ![]() -
натуральное число.
-
натуральное число.
Отметим еще одно
важное неравенство между нормами матриц ![]() и
и ![]() одинакового типа. Применяя условие в),
будем иметь:
одинакового типа. Применяя условие в),
будем иметь:
![]()
Отсюда
![]()
Аналогично
![]()
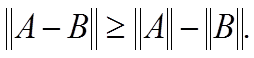
Следовательно,
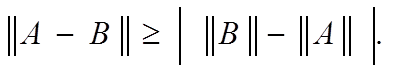
Назовем норму канонической, если дополнительно выполнены условия:
д) если 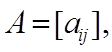 то
то
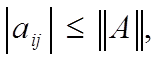
причем для скалярной матрицы 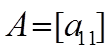 имеем
имеем 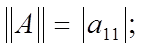
е) из неравенства 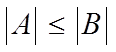 (А и В – матрицы ) следует неравенство
(А и В – матрицы ) следует неравенство
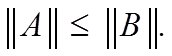
В частности, 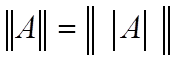 .
.
В дальнейшем для матрицы 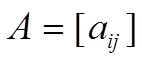 произвольного типа мы будем
рассматривать главным образом три легко вычисляемые нормы:
произвольного типа мы будем
рассматривать главным образом три легко вычисляемые нормы:
1) 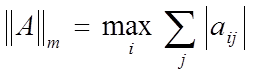 (m – норма);
(m – норма);
2) 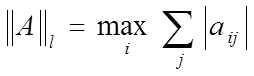 (
(![]() - норма);
- норма);
3) 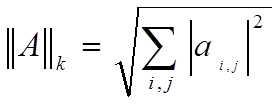 (
(![]() - норма).
- норма).
П р и м е р. Пусть
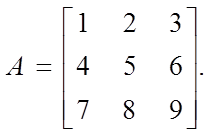
Имеем:
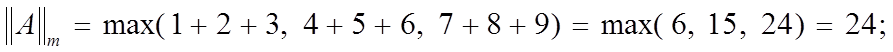
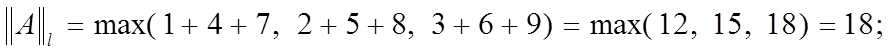
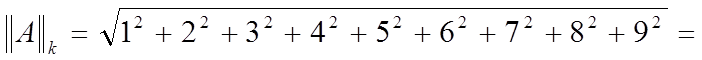
![]()
§ 9. Предел матрицы
 (1)
(1)
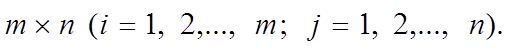
Под пределом последовательности
матриц ![]() понимается матрица
понимается матрица
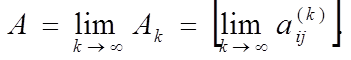 (2)
(2)![]()
Последовательность матриц, имеющая предел ,называется сходящейся.
Л
е м м а 1. Для сходимости последовательности матриц к матрице ![]() (к =1,2,…) к матрице А необходимо и
достаточно, чтобы
(к =1,2,…) к матрице А необходимо и
достаточно, чтобы
![]() при
при
![]() (3)
(3)
где![]() любая коническая
норма матрицы А. При этом
любая коническая
норма матрицы А. При этом
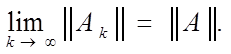
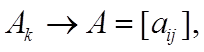
то
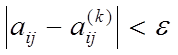 при
при ![]()
![]()
Отсюда
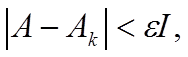
где
I – матрица
типа ![]() , все элементы которой равны единице.
, все элементы которой равны единице.
В силу свойств нормы имеем:
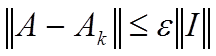 при
при ![]()
следовательно,
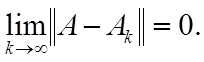
Обратно,
пусть выполнено условие (3). Тогда при ![]() имеем:
имеем:
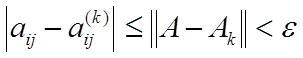
и, следовательно,
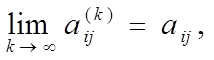
т. е.
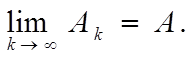
Кроме
того, если ![]() то имеем:
то имеем:
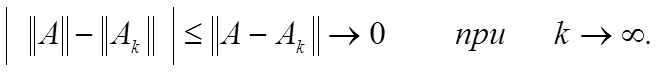
Поэтому
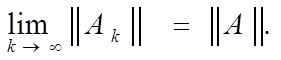
С
л е д с т в и е. Последовательность 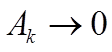 при
при ![]() тогда и только тогда, когда
тогда и только тогда, когда
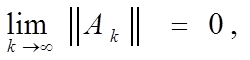
где
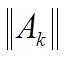 какая-нибудь каноническая норма.
какая-нибудь каноническая норма.
Легко убедиться, что если
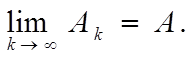 и
и 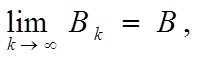
то:
a) 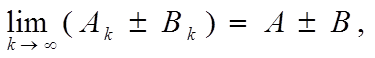
б) 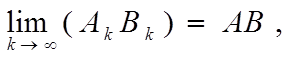
в)
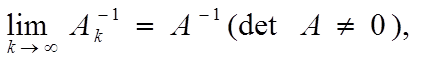
в
предложении, что соответствующие операции имеют смысл. В частности, если ![]() – постоянная матрица такая, что возможны
перемножения
– постоянная матрица такая, что возможны
перемножения ![]() и
и ![]() то
то
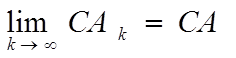
и
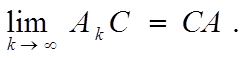
Л
е м м а 2. Для сходимости последовательности
матриц 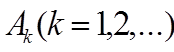 необходимо и достаточно, чтобы был
выполнен обобщенный критерий Коши, а именно: для всякого
необходимо и достаточно, чтобы был
выполнен обобщенный критерий Коши, а именно: для всякого ![]() должен существовать такой номер
должен существовать такой номер ![]() что при
что при ![]()
где
![]() - любая каноническая норма.
- любая каноническая норма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.