ПОЯСНИЕ К ПРОГРАММЕ
И ИНСТРУКЦИЯ ПО ПОЛЬЗОВАНИЮ
ПЛАН
1. Постановка задачи.
2. Математическая модель.
3. Описание и алгоритм реализации программы
4. Инструкция по пользованию.
5. Полученный результат.
6. Системные требования.
7. Литература.
------------------------------------------------------------------------------------------------------------
1.Данная программа даёт нам численное решение итерационных уравнений методом Ньютона.
Пограмма решает итерационные уравнения третьего порядка вида
Y = F( X )
Программа реализована в среде BorlandPascalforWindows.
2.Матеметическая модель задачи :
Метод Ньютона (метод касательных) для приближенного решения уравнения F(x)=0
состоит в построении итерационной последовательности {xn},n=0,1,2,...,которая сходиться к корню уравнения на отрезке[a,b] его локализации.
На рисунке (см. ниже) изображено способ получения первого приближения по методу касательной: x1 это точка пересечения касательной, проведённой к точке с координатами (x0,f(x0)) .Из прямоугольного треугольника ,острый угол которого а
Имеем Tg(
)=f ’(x0
)= 
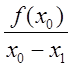;откуда x
= x
-
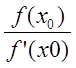
Достаточные условия схождения такие.Пусть f(x) определённа на [a,b],
Причём производные f ’(x) и f ‘’(x) сходятся на [a,b].Тогда, исходя из начального приближения x0є[a,b], которое удовлетворяет неравенство
f(x0)f ”(x0)>0,итерационная
последовательность x
=x
-
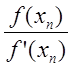
сходится к единому на [a,b] решению ₤ уравнения f(x)=0.
Для оценки погрешности n-нного корня можно воспользоваться неравенством
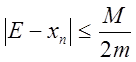
Где М это наибольшее значение модуля второй производной на [a,b];
М это наименьшее значение модуля первой производной на [a,b];
При необходимости вычислить корень с точностью ℮ итерационную последовательность прерывают при условии
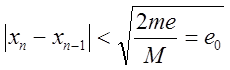
Метод Ньютона еффективен, если выбранно удачное начальное приближение
Для корня и в окрестностях корня график имеет большую крутость.
3. Описание и алгоритм реализации программы :
В этой программе использованы такие стандартные модуля, как WinCrt,
WinProcs, WinTypes. Подключение двух последних модулей дало нам доступ к APIфункциям, что позволило работать с графикой (вычерчивание таблицы) .
Наиболее часто употребляемый оператор – это IF
If<условие> then ... else...
Алгоритм решения задачи :
1) Вывод информации на экран. Это описано в процедуре OKNO. Она вызывается первой в программе.
2) Ввод данных. За это отвечает процедура VVOD. В этой процедуре описаны переменные, которые нужно ввести, а также условия ввода.
3) Реализация алгоритма. Это самая главная часть программы.
В процедуре ALGOR производится расчёт значений X и Y.
4)Вывод результата осуществляется процедурой VIVOD.
5) Сохранение результатов осуществляется процедурой SAVE.
Все перечисленные процедуры,функции находятся в модуле MODUL Также в этом модуле находится описание всех типов, констант и переменных.
4.Инструкция по пользованию :
Перед компиляцией программы необходимо создать текстовый файл в папке User : ‘C:\User\in-22\Rezult.txt’.
Необходимо ввести :
а) границы отрезка итерационной последовательности А и В(А<Б);
б)коэффициенты и свободный член уравнения;
в)точность вычислений.
5.Результат :
Результат можно сохранить втекстовом файле.
6. Системные требования :
Windows 95 / 98 / Millenium /XP ;
8 Mb RAM ;
0.1 Mb HDD.
7. Список литературы :
1. Культин Н.Б. Программирование в Turbo Pascal 7.0 и Delphi. – СПб.:
2. Сурков Д.А., Сурков К.А., Вальвачев А.Н. Программирование в среде Borland Pascal для Windows. – Минск: Высш. шк., 1996. – 432 с.
3.Вычислительная техника в инженерных и экономических расчетах.Под ред.
Петрова А.В.-Москва:Высш.шк.,1984.-320.с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
