Чисельний пошук екстремуму функції однієї змінної. Чисельні методи пошуку екстремуму функції декількох змінних, страница 2

  6  f(x)=+x² ,                                         [0;1].

  7  f(x)=-1/x,                                    [-1;-0,5].

  8  f(x)=+ln(x),                                       [1 ;3].

  9  f(x)=+1/(1-x),                            [-0,5;0,5].

10  f(x)=-tg(x)-1/x,                                   [-1;-0,5].

11  f(x)=+x² ,                                          [-1;0].

12  f(x)=+1/x,                                        [0,5;1].

13  f(x)=-ln(x),                                       [0,3;1].

14  f(x)=+1/(x+1),                             [-0,5;0,5].

15  f(x)=tg(x)+1/x,                                      [0,5;1].

16  f(x)=tg(x)++x,                                 [-1;0].

17  f(x)=x²+sin(x),                                        [-1;0].

18  f(x)=-sin(x),                                         [0;1].

19  f(x)=x⁴+2x²+4x,                                     [-1;0].

20  f(x)=x+x² ,                                         [-1;0].

21  f(x)=-tg(x)-x,                                       [0;1].

22  f(x)=x²-sin(x),                                           [0;1].

23  f(x)=+sin(x),                                     [-1;0].

24  f(x)=x⁴+2x²-4x,                                         [0;1].

25  f(x)=x²-x,                                            [0;1].

26  f(x)=x+(2-x)/x² ,                                    [0,5;1].

27  f(x)=1/x-1/ln(x),                                  [0,3;0,7].

28  f(x)=1/x+ln²(x),                                        [1;3].

29  f(x)=+ln(x),                                         [1;3].

30  f(x)=+1/x,                                     [0,5;1,5].

Глава 10

 Чисельні методи пошуку екстремуму функції декількох змінних

Методи мінімізації (максимізації) функції можуть бути по-ділені на прямі та непрямі. У прямих методах пошук точки екстре-муму починається з довільної точки і провадиться шляхом послі-довного її покращання. У непрямих методах точки екстремуму знаходять з необхідної умови його існування

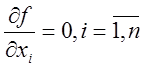                                      (10.1)

10.1 Метод Ейлера.

Цей метод належить до непрямих методів. Для його реаліза-ції треба застосувати вищезгадану необхідну умову існування екс-тремуму та перевірити достатню умову. Вимогами цієї умови є до-слідження матриці Гессе G , обчисленої в точці , де ,за допомогою критерію Сільвестра:

G=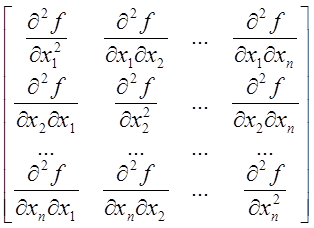                     (10.2)

Якщо всі головні мінори такої матриці (10.2) додатні, то точка  є точкою мінімуму.

Якщо ж головні мінори непарного порядку від’ємні, а парного – додатні, то точка є точкою максимуму ( головні мінори матриці містять на їх головних діагоналях елементи голов-ної діагоналі матриці ).

Приклад. Знайти екстремум функції

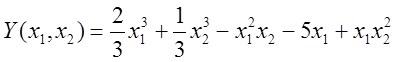
Користуючись необхідною умовою пошуку екстремуму отримаємо систему рівнянь

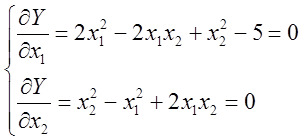
Розв’язуючи її, одержимо стаціонарні точки:

   

Для дослідження характеру цих точок застосуємо критерій Сильвестра для матриці Гессе:

  

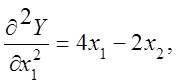
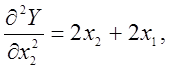
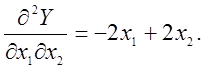
Матриця Гессе для точки

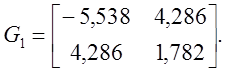
Головні мінори  . Отже, у цій точці екстремуму немає.

Матриця Гессе для точки

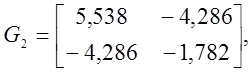
 Екстремум відсутній також.

Матриця Гессе для точки

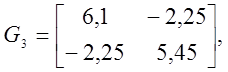
  За критерієм Сільвестра у функції в цій точці мінімум

Матриця Гессе для точки

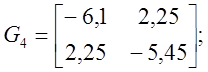
  Функція досягає максимуму

10.2 Метод градієнтного спуску

Цей метод належить до прямих методів пошуку мінімуму функції X), де X=(), і полягає у побудові послідовно-сті точок  , що задовольняють умову

.

Вибираємо початкову стартову точку , знаходимо напрямок найбільшого спадання функції у цій точці і робимо в ньому  один крок; приходимо до точки  , у точці повторюємо процедуру, знаходимо і т.д. Довжина кроку залишається довільною , її теж можна відшукати за умови, щоб у кожній точці  функція набере мінімального значення.