Чисельний пошук екстремуму функції однієї змінної. Чисельні методи пошуку екстремуму функції декількох змінних, страница 4

Приклад. Довжина дуги  кривої , яка визначена на  та диференційована в

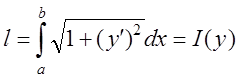                               (11.1)

буде функціоналом від однієї функціональної змінної.

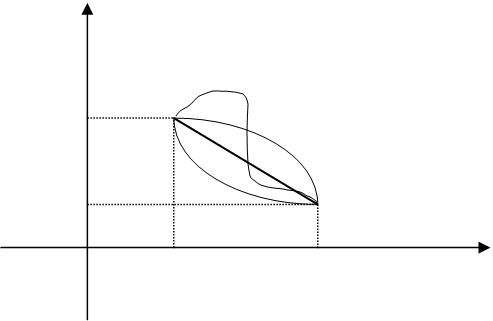
Для функціонала (11.1) поставимо задачу на екстремум функціонала. Серед всіх неперервних диференційованих функцій , для яких  знайти ту, довжина дуги якої має найменше можливе значення, тобто знайти таку функцію , яка надає інтегралу (11.1) мінімум. Зрозуміло, що розв’язком є лінійна функція, тобто пряма, що з’єднує точки А і В ( рисунок 11.1):

 

                                  y

                                 y_a                  A

                                 y_b                                                          B

                                 O             a                       b                   x

Рисунок 11.1

              Варіаційне числення є частиною вищої математики, де розглядаються умови екстремуму функціонала.

11.1 Екстремум функціонала

            Екстремуми функціоналів так само, як і екстремуми функ-цій зі скінченним числом незалежних змінних, можуть бути глобальними і локальними залежно від того, шукаємо екстремум функціонала на всьому класі функцій, для яких існує функціонал, чи на його частині. У подальшому буде розглядатися локальний

 екстремум функціонала:

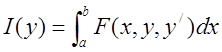                              (11.2)

у класі функцій y(x) із закріпленими кінцями  таких, що

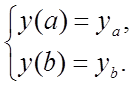                                      (11.3)

До класу  належать неперервні разом з першою похідною для  функції , для яких введена норма

.

Для функціонала  (11.2) роль аргумента виконує функція . Тому приріст аргумента можна визначити за анало-гією з приростом аргументу функції як різницю між двома різними функціями при одному й тому ж аргументі самих функцій. При-ріст аргумента функціонала називається варіацією функції і позначається .За визначенням

.                    (11.4)

Варіація похідної функції визначається як

.

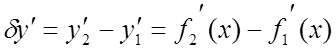Приріст функціонала є аналогом приросту функції:

.                      (11.5)

Якщо приріст функціонала може бути поданий у вигляді

,                      (11.6)

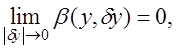де  а  є лінійним функціоналом відносно , то  називається варіацією функціонала:

.                                (11.7)

Отже, варіація функціонала однієї функціональної змінної – це головна лінійна по відношенню до , частина приросту функціонала.

            Як відомо, необхідна умова екстремуму функції полягає у тому, що диференціал першого порядку дорівнює нулю . За анало-гією, якщо функціонал досягає екстремуму на деяких функціях , то на цих функціях варіація першого порядку від функціонала дорівнює нулю:

                              (11.8)

11.2 Диференціальні рівняння екстремалей

Поставимо завдання отримати необхідну умову екстремуму функціонала (11.2),що розглядається на класі функцій із закріпле-ними кінцями (як на рисунку 11.1). Тобто клас допустимих функ-цій обмежують додатковими умовами (11.3).

Приріст функціонала

.

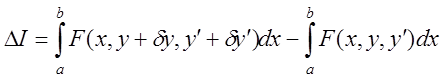Розвинемо функцію  в ряд Тейлора в околі точки :

.

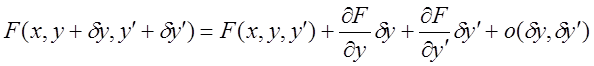Тоді варіація функціонала як головна частина його прирос-ту матиме вигляд

.

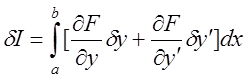Застосуємо до другого доданка

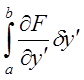
метод інтегрування за частинами. Враховуючи, що , в результаті з необхідної умови існування екстремуму отримаємо

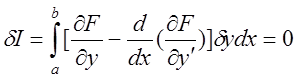.                          (11.9)

Це можливо, якщо виконується

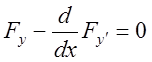                                         (11.10)

- рівняння  Ейлера  для  функціонала ( диференціальне  рівняння  2-го порядку щодо функції у(х)). Тут .

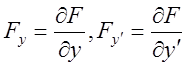До нього необхідно додати граничні умови :