Решение задачи предполагает выбор вами одной из денежных сумм – $1000 сегодня или $2000 через 8 лет. Проблема выбора одной из вышеуказанных сумм состоит в том, что эти суммы находятся в разном времени. $1000 вы можете «взять» сейчас, сегодня, а чтобы «взять» $2000 вам надо ждать 8 лет, после чего вы их можете “получить”. Естественно, вы будете выбирать большую сумму денег. Поэтому нужно узнать какая из сумм денег больше – $1000 сегодня или $2000 через 8 лет.
В связи с тем, что СТОИМОСТЬ ДЕНЕГ ИЗМЕНЯЕТСЯ ВО ВРЕМЕНИ, сравнивать $1000 сегодня и $2000 через 8 лет можно только при условии, что сравниваемые суммы находятся в одном и том же времени.
Условие задачи можно изобразить графически (рис. 1):
9% 9% 9% 9% 9% 9% 9% 9%
Годы 0 1 2
3 4 5 6 7 8
Деньги $1000 $2000
Рисунок 1
На рисунке 1 изображена временная ось. Точка 0 обозначает начало первого года (это и ест наше «сегодня»), точка 1 – конец первого года и начало второго, точка 2 – конец 2-го года и начало 3-го и т.д. Точка 8 – конец 8-го года (это и есть наше «будущее»). Из условия задачи – ставка процентная, начисление процентов – ежегодное.
Для выяснения вопроса, какая из сумм больше – $1000 сегодня или $2000 через 8 лет, механизм расчета следующий: $1000 сегодня мы пересчитываем в будущее время – на конец 8-го года и после этого пересчета будущую стоимость $1000 сравниваем с $2000, т.е. выясняем, какая из сумм больше.
Решение задачи
Находим стоимость $1000 через 8 лет. Другими словами, находим, какой
суммой станет $1000, если ее положить в банк на срок 8 лет под 9% годовых с
ежегодным сложным начислением процентов. Используем формулу (6) 
.
FV1000 = $1000(1+0,09)8 = $1992,56 .
Расчет показывает, что будущая стоимость $1000 через 8 лет будет равна $1992,56. Величина $1992,56 может сравниваться, сопоставляться с величиной $2000, т.к. эти величины находятся в одном времени. Следовательно, $2000 через 8 лет предпочтительнее, чем $1000 сегодня, конечно, если условия задачи будут выполнены.
Эта задача может быть решена другим способом.
Находим стоимость $2000 сегодня. Другими словами, находим, какую сумму надо было бы иметь сегодня, чтобы положив ее в банк на 8 лет под 9% годовых с ежегодным сложным начислением процентов, получить через 8 лет $2000.
Для решения этого вопроса используем формулу (9)
,
.
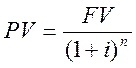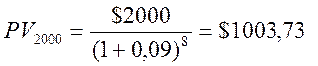Расчет показывает, что настоящая стоимость $2000 равна $1003,73. Величина $1003,73 может сравниваться, сопоставляться с величиной $1000, т. к. эти величины находятся в одном времени. Следовательно, $2000 через 8 лет предпочтительнее, чем $1000 сегодня, конечно, если условия задачи будут выполнены.
Ответ. $2000 через 8 лет предпочтительнее, чем $1000 сегодня.
При решении задачи 4 мы ПЕРЕВОДИЛИ (пересчитывали) стоимость $1000 сегодняшнюю в будущую стоимость, а при решении вторым способом будущую стоимость $2000 ПРИВОДИЛИ (пересчитывали) в стоимость настоящую, или, как ее называют финансисты, текущую. Таким образом, можно сделать вывод, что ПЕРЕВЕДЕНИЕ стоимости и ПРИВЕДЕНИЕ стоимости – это ПЕРЕСЧЁТ стоимости по формулам (5), (6), (7), (8), (9) в зависимости от условий пересчёта.
Пересчёт стоимости из настоящего момента времени к определенному моменту в будущем называется МУЛЬТИПЛИКАЦИЯ. Формулы (5), (6), соответствующие такому пересчёту, называются МУЛЬТИПЛИКАТИВНЫМИ. Пересчёт будущей стоимости к настоящему моменту времени называется ДИСКОНТИРОВАНИЕМ. Следовательно, дисконтный пересчёт предполагает использование формул (7), (8), (9).
Формула (9) имеет самостоятельное значение и трактуется в расчетах, как
ФОРМУЛА ПРИВЕДЕНИЯ. Безразмерный коэффициент в этой формуле в виде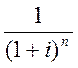 
- называется КОЭФФИЦИЕНТОМ ДИСКОНТИРОВАНИЯ
или, как часто встречается в литературе, ДИСКОНТОМ.
5 СМЕШАННОЕ НАЧИСЛЕНИЕ ПРОЦЕНТОВ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.