Как видно из модельных задач 1 и 2, разные схемы начисления процентов приводят одинаковые базовые условия вклада (сумма вклада - 1000 грн) к совершенно различным конечным суммам денег. Схема простых процентов дает, в итоге 1400 грн., а схема сложных процентов – 1464,1 грн.
Видим, что схема сложных процентов дает большую будущую стоимость. Поэтому финансисты всего мира считают будущую стоимость по сложной схеме начисления процентов, если иное не оговорено в условиях.
Ö ЗАПОМНИТЕ: ЕСЛИ В УСЛОВИЯХ НЕ ОГОВАРИВАЕТСЯ СХЕМА НАЧИСЛЕНИЯ ПРОЦЕНТОВ (СЛОЖНАЯ ИЛИ ПРОСТАЯ), ТО ВСЕГДА РАСЧЕТ ВЕДЕТСЯ ПО СЛОЖНОЙ СХЕМЕ НАЧИСЛЕНИЯ ПРОЦЕНТОВ.
Формулы (5) и (6) используются для расчетов с использованием процентных ставок. Если же необходимо выполнить расчет с использованием учетных, ставок то пользуются формулами (7), (8).
Формула начисления простых процентов при использовании учетной ставки:
![]() ,
(7)
,
(7)
где d –учётная ставка в каждом из n периодов начисления процентов. Значение символов PV, FV, n –то же, что и в формуле (5).
Формула начисления сложных процентов при использовании учетной ставки
![]() .
(8)
.
(8)
Суть символов PV, FV. n, d– та же, что и в формуле (7)
Ö ЗАПОМНИТЕ: ЕСЛИ В УСЛОВИЯХ НЕ УКАЗАНО, КАКУЮ СТАВКУ – УЧЕТНУЮ ИЛИ ПРОЦЕНТНУЮ – ИСПОЛЬЗОВАТЬ ПРИ РАСЧЕТЕ, ТО ПОДРАЗУМЕВАЕТСЯ ИСПОЛЬЗОВАНИЕ ПРОЦЕНТНОЙ СТАВКИ(формулы(5),(6)).Закрепим полученные знания на примере решения следующих задач
Задача 1
Рассчитайте наращенную сумму с исходной суммы в 2 млн. грн при размещении ее в банке на срок 10 лет на условиях начисления: а) простых; б) сложных процентов, если годовая ставка 15%, а периоды наращения (начисления) такие:
- квартал;
- полугодие;
- один год;
- 5 лет;
- 10 лет.
Для решения поставленной задачи требуется произвести 10 расчетов и получить 10 значений величины FV. Годовая процентная ставка – 15%.
Решение задачи
Условие начисления процентов – простое (вариант а).
1) ежеквартальное начисление процентов (формула (5)):
Для начала подготовим данные, входящие в формулу (5) к нашим условиям задачи: PV = 2 млн. грн., n рассчитаем из знания того, что год имеет 4 квартала, а общее количество лет вклада 10. Следовательно, количество периодов начисления n = 40, процентная ставка в условии задачи дается как годовая, следовательно, для квартала процентная ставка i=0,15/4. Подготовленные значения подставим в формулу (5), получим
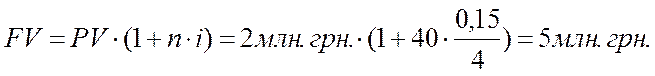
2) полугодовое начисление процентов (формула (5)):
n рассчитаем из знания того, что год имеет 2 полугодия, а общее количество лет вклада 10. Следовательно, количество периодов начисления n=20, процентная ставка в условии задачи дается как годовая, следовательно, для полугодия процентная ставка i=0,15/2. Подготовленные значения подставим в формулу (5), получим
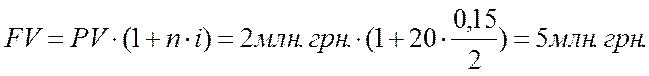
3) годовое начисление процентов (формула (5)):
n = 10, i = 0,15 Подготовленные значения подставим в формулу (5), получим:
![]()
4) начисление процентов раз в 5 лет (формула (5)):
n рассчитаем из знания того, что в 10 годах есть 2 периода по 5 лет. Следовательно, количество периодов начисления n=2, процентная ставка в условии задачи дается как годовая следовательно, для пятилетнего периода процентная ставка i = 0,15*5. Подготовленные значения подставим в формулу (5), получим
![]()
5) начисление процентов раз в 10 лет (формула (5)):
n рассчитаем из знания того, что в 10 годах содержится 1 период из 10 лет. Следовательно, количество периодов начисления n=1, процентная ставка в условии задачи дается как годовая следовательно, для десятилетнего периода процентная ставка i = 0,15*10. Подготовленные значения подставим в формулу (5), получим:
![]()
Условие начисления процентов – сложное (вариант б).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.