6) ежеквартальное начисление процентов (формула (6)).
Для начала подготовим данные, входящие в формулу (6) к нашим условиям задачи: PV = 2 млн. грн., n рассчитаем из знания того, что год имеет 4 квартала, а общее количество лет вклада 10. Следовательно, количество периодов начисления n =40, процентная ставка в условии задачи дается, как годовая, следовательно для квартала процентная ставка i=0,15/4. Подготовленные значения подставим в формулу (6), получим:
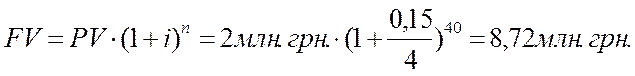
7) полугодовое начисление процентов (формула (6)):
n рассчитаем из знания того, что год имеет 2 полугодия, а общее количество лет вклада 10. Следовательно, количество периодов начисления n=20, процентная ставка в условии задачи дается, как годовая, следовательно, для полугодия процентная ставка i=0,15/2. Подготовленные значения подставим в формулу (6), получим
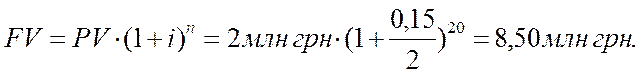
8) годовое начисление процентов (формула (6)):
n = 10, i = 0,15 подготовленные значения подставим в формулу (6), получим
![]()
9) начисление процентов раз в 5 лет (формула (6)):
n рассчитаем из знания того, что в 10 годах есть 2 периода по 5 лет. Следовательно, количество периодов начисления n=2, процентная ставка в условии задачи дается как годовая, следовательно для пятилетнего периода процентная ставка i=0,15*5. Подготовленные значения подставим в формулу (6), получим
![]()
10) начисление процентов раз в 10 лет (формула (6)):
n рассчитаем из знания того, что в 10 годах содержится 1 период из 10 лет. Следовательно, количество периодов начисления n=1, процентная ставка в условии задачи дается как годовая, следовательно, для десятилетнего периода процентная ставка i = 0,15*10. Подготовленные значения подставим в формулу (6), получим
![]()
Анализируя приведенную задачу, можно сделать следующие выводы:
ВЫВОД 1: При начислении простых процентов разбиение срока вклада на периоды начисления не влияет на величину наращенной суммы.
ВЫВОД 2: При начислении сложных процентов разбиение срока вклада на периоды начисления влияет на величину наращенной суммы. Более частое начисление сложных процентов обеспечивает более быстрый рост наращиваемой суммы.
Задача 2
Банк предлагает 20% годовых. Чему должен быть равен первоначальный вклад, чтобы через 3 года иметь на счете 5 млн. грн.
Известно, что FV = 5 млн грн. Схема начисления процентов не указана, следовательно – сложная. Вид ставки не оговаривается, следовательно, ставка – процентная. Периоды начисления не оговариваются, следовательно, период начисления – ежегодно. Тогда i=20%, n=3. Найти величину PV.
Используем формулу (6), в которой неизвестной величиной есть PV.
![]()
Из этой формулы выразим PV, получим
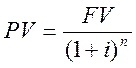 . (9)
. (9)
Подставляем исходные данные и получаем ответ
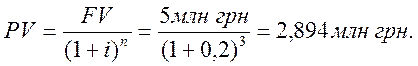
Ответ для того, чтобы через 3 года иметь на счете 5 млн грн при процентной ставке 20% необходимо положить в банк на счет 2,894 млн грн.
Задача 3
Стратегия решения
Известно, что PV = 10 млн грн. Схема начисления процентов не указана, следовательно – сложная. Периоды начисления не оговариваются, следовательно, период начисления – ежегодно. Тогда n = 5, FV = 20 млн. грн. Найти величину i.
Используем формулу (6) в которой неизвестной величиной есть i
![]() .
.
Из этой формулы выразим i, получим
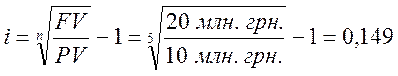
Ответ для того чтобы удвоить 10 млн грн через 5 лет необходимо их положить на депозитный счет под минимально приемлемую ставку, равную 14,9%.
4 ПРИВЕДЕННАЯ СТОИМОСТЬ
В финансах часто используется понятие ПРИВЕДЕННАЯ СТОИМОСТЬ. Суть этого понятия раскроем на примере решения задачи 4.
Задача 4
Какая сумма денег для вас предпочтительнее при годовой процентной ставке 9%: $1000 сегодня или $2000 через 8 лет?
Стратегия решения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.