Методичні вказівки до лабораторних занять з дисципліни "Стандартизація та сертифікація в галузі захисту інформації", страница 27

Відповідно до формул кон’юнкції обчислимо значення b, d, u для Критичних елементів 2.1 і 7.2. Об'єднання думок будемо проводити методом ітерацій, тобто параметр (довіра, недовіра, невизначеність) першого поєднується з параметром другого, а їхній результат з параметром наступного.

Після проведення обчислень маємо:

Критичний елемент 2.1: b = 0,075;  d = 0,69;  u = 0,235.

Критичний елемент 7.2: b = 0,18;  d = 0,52;  u = 0,3.

Аналіз отриманого результату вказує на те, що Критичний елемент 7.2 заслуговує більшої довіри (більш ніж у 2 рази),а рівень недовіри в нього нижче, ніж у Критичного елемента 2.1, при майже однакових значеннях параметра невизначеності. Така оцінка не є правомірною. У дійсності, твердження Критичного елемента 2.1 оцінювалися як ті що заслуговують більш високого рівня довіри, з низьким рівнем невизначеності. 

Дана помилка показує, на некоректність застосування операції кон’юнкції для n>2. Таким чином, необхідно вирішити другу проблему використання апарата суб'єктивної логіки.

Постановка задачі на розробку  оператора об'єднання  

Нехай кількість тверджень n, w_р – думка оцінювача відносно р-го твердження, що можна уявити у виді w_p = {b_p, d_p, u_p},  де b_p  - рівень довіри до  р-ого  твердження, d_p - рівень недовіри до р-ого твердження, u_p - рівень невизначеності, наявної відносно  р–ого  твердження. Нехай w_Sn - об'єднана адекватна думка по n твердженнях, що можна уявити у виді

w_Sn  = {b_Sn,  d_Sn ,  u_Sn },

де b_Sn  - рівень довіри до  n  тверджень;

    d_Sn - рівень недовіри до  n  тверджень;

    u_Sn  - рівень невизначеності  відносно  n тверджень.

Необхідно знайти такий оператор об'єднання f(W_n) – де W_n – безліч думок відносно n тверджень, що w_Sn =f(W_n) .

 Рішення даної задачі можливо за допомогою наступних шляхів:

1)  Введення деякого поправочного коефіцієнта k як функції від числа (n);

2)  Застосування замість кон’юнкції середнього значення параметрів;

3)  Знаходження середнього значення кон’юнкції для n думок.

Рішення задачі має задовольняти ти таким вимогам:

-  результат має залежати від чисельних значень параметрів думок, а не від їхньої кількості;

-  результат не повинний суперечити положенням суб'єктивної логіки.

Введення  поправочного коефіцієнта.

Нехай w¹_Sn  = {b¹_Sn, d¹_Sn , u¹_Sn} - об'єднана думка отримана методом послідовних ітерацій, а w_Sn -   думка така, що адекватно відображає істинність Критичного Елемента, що включає n – тверджень. Тоді суть уведення поправочного коефіцієнта полягає в обчисленні таких коефіцієнтів K_b(N), K_d(N), K_u(N), що

w_Sn= {K_b(N)* b_Sn ,  K_d(N)* d_Sn , K_u(N)* U_Sn}

Залежність поправочних коефіцієнтів від кількості поєднуваних тверджень  буде носити нелінійний характер. Складність знаходження і той факт, що такі коефіцієнти швидше за все будуть нівелювати значення окремих параметрів, фактично спираючись на мінімальні і максимальні значення параметрів, не дозволяє використовувати даний метод у якості прийнятного оператора об'єднання

    Середнє значення параметрів

Використання даної методики має на увазі застосування середнього арифметичного значення параметрів. Обчислення підсумкових значень параметрів відбувається по формулах 

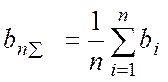
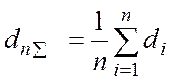                                               (А.2)

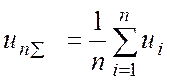
Після проведення обчислень маємо наступні оцінки:

Критичний елемент  2.1:  b = 0,63;  d = 0,2;  u = 0,17.

Критичний елемент  7.2: b = 0,45;  d = 0,3;  u = 0,25.

Даний метод хоча і позбавлений від недоліку методу послідовних ітерацій – залежності об'єднаних кон’юнкції від кількості поєднуваних думок, але при цьому він не відповідає положенням суб'єктивної логіки. Тому що подібна оцінка не враховує залежностей між твердженнями і не відповідає жодному визначеному для суб'єктивної логіки оператору. 

Усереднена попарна  кон’юнкція