Методичні вказівки до лабораторних занять з дисципліни "Стандартизація та сертифікація в галузі захисту інформації", страница 19

У даному підрозділі розглядається математичний апарат суб’єктивної логіки, застосування якого дозволяє висловлювати і оброблювати думки експерта, за допомогою спеціальних операторів, які моделюють розумову діяльність людини.

Стандартна логіка оперує на двійкових змінних, які можуть приймати дискретні значення «ІСТИНА» та «БРЕХНЯ». Суб'єктивна логіка оперує з думками, представленими у вигляді вектору .

Думки, як і свідчення, розглядаються індивідуально і таким чином, вони обов’язково належать комусь і виносяться до чогось (чи когось). Думка експерта А про істинність (правдивість, вірогідність) твердження  позначається як .

У суб'єктивній логіці визначено 7 операторів обробки думок:

–  кон’юнкція (об'єднання) думок;

–  диз'юнкція (роз'єднання) думок;

–  заперечення думки;

–  незалежний консенсус;

–  залежний консенсус;

–  частково залежний консенсус;

–  рекомендація.

2.3.3.1 Кон’юнкція

Формування кон’юнкції двох тверджень з сфокусованих фреймів розрізнення полягає у виробленні з двох думок стосовно кожного твердження, нової думки, що буде виражати віру в істинність обох тверджень одночасно. Цей оператор є аналогом “AND” у бінарній логіці.

Теорема 3 (Кон’юнкція тверджень)

Нехай  та  це два бінарних сфокусованих фрейму розрізнення,  та - відповідно твердження стосовно станів в  та . Тоді  та , це думки відносно цих станів, нехай  така думка, що

1. ;

2. ;

3.  

4. ;

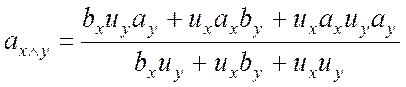Тоді  має назву кон’юнкція тверджень думок  та  і виражає думку особи, яка приймає рішення стосовно того, що обидва твердження  та є істинними. Для позначення цього оператора використовується символ  таким чином

2.3.3.2 Диз'юнкція

Формування диз'юнкції двох тверджень зі сфокусованих фреймів розрізнення полягає у визначенні з двох думок стосовно кожного твердження нової думки, яка буде виражати віру в істинність або одного твердження або їх одночасну істинність. Цей оператор є аналогом “OR” у бінарній логіці.

Теорема 4 (Диз'юнкція тверджень)

Нехай  та  це два бінарних сфокусованих фрейму розрізнення,  та - відповідно твердження стосовно станів в  та . Тоді  та  це думки відносно цих станів. Нехай  така думка, що

1. ;

2. ;

3. ;

4. .

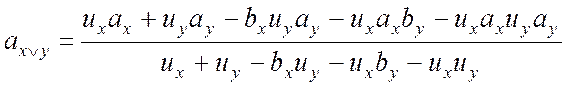Тоді  має назву кон’юнкція тверджень думок  та  і виражає думку особи, яка приймає рішення стосовно того, що або обидва одне з тверджень  або є істинними, або вони істині разом. Для позначення цього оператора використовується символ  таким чином

2.3.3.3 Заперечення

Заперечення думки щодо твердження  визначає думку, що  буде неістинне. Ця операція є аналогом заперечення “NOT” у бінарній логіці.

Теорема 5 (Заперечення)

Нехай  це думка відносно . Тоді  це заперечення  де:

1.;

2.

3.

4. .

Заперечення є інволютивним, тобто  вірно для будь-якої думки .

2.3.3.4 Консенсус між незалежними думками

Консенсус між двома думками об’єднує їх, вважаючи, що вони незалежні та мають однакове значення. Наприклад, якщо два експерта спостерігали за певним явищем у два проміжки часу, що не перекриваються, вони можуть мати про нього різні думки. Консенсус дозволяє сформувати нову думку, що повинна дорівнювати думці третього експерту (віртуального експерту), який нібито спостерігав це явище у обидва проміжки часу.

Теорема 6 (Заперечення)

Нехай  і  думки, що належать відповідно експертам А и В, відносно твердження р. Нехай  буде думкою такою, що

1.;

2.;

3.  .

4. ;

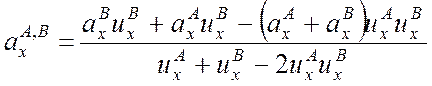де  причому та .

Операція консенсусу є комутативною й асоціативною, отже порядок комбінування думок не важливий. Передбачається, що думки незалежні. Не можна врахувати думки більш ніж один раз.

Дві думки, що містять нульову невизначеність, відповідно до теореми 1 не можуть комбінуватися. Це можна пояснити через ітерацію невизначеності “як кімната для впливу”, тобто виникає можливість уплинути на думки, які ще не були висловлені ні за, ні проти твердження. Ситуація з незалежними абсолютно визначеними думками, з філософської точки зору, безглузда, по-перше тому, що думки не можуть бути абсолютно визначеними і по-друге, вони тоді повинні бути обов'язково однаковими.