Методичні вказівки до лабораторних занять з дисципліни "Стандартизація та сертифікація в галузі захисту інформації", страница 10

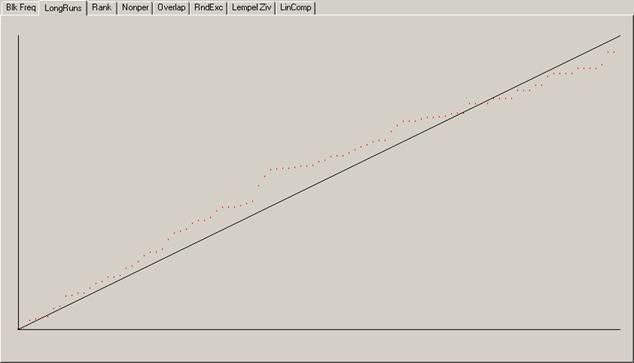
Рисунок 1.10  а) – Побудова функції розподілу

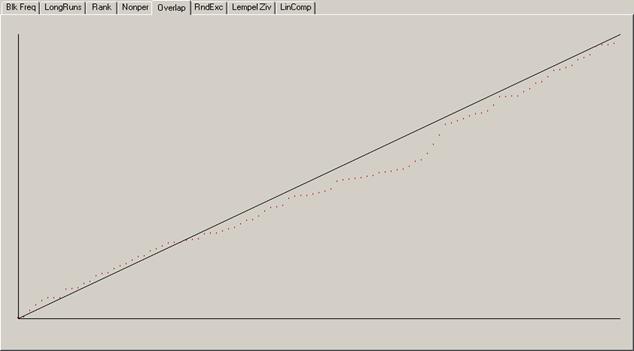
Рисунок 1.10  б) –Побудова функції розподілу

Після закінчення роботи програми всі сумарні розрахункові дані розміщуються в кореневому каталозі у файлі finalAnalysisReport. На рис 1.11 представлений типовий звіт програмного модулю щодо тестування псевдо випадкової послідовності шляхом застосування частотного тесту (frequency test), тесту сум накопичення (cusum test) та тесту серій (serial test).

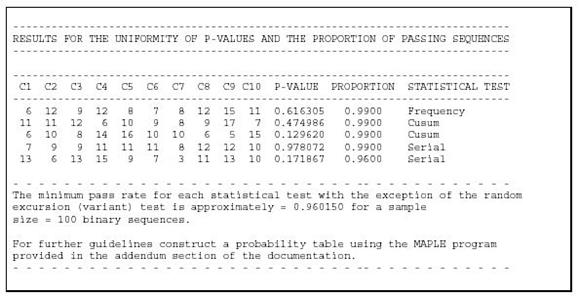
Рисунок 1.11 – Типовий звіт програмного модулю

У разі якщо послідовність не пройшла тест, біля його назви відображається зірочка. Для більш детального аналізу кожного проходження послідовністю кожного тесту можна використати файли, що знаходяться у поточному каталозі \experiments\AlgorithmTesting\Назва тесту, що цікавить.

1.5 Завдання на лабораторну роботу

Провести статистичні випробування визначених генераторів випадкових та псевдовипадкових послідовностей за методикою NIST STS. Провести аналіз отриманих результатів та сформувати акт випробувань.

1.5.1 За допомогою спеціального програмного забезпечення сформувати псевдовипадкову послідовність.

1.5.2 Провести тестування із використанням лабораторної установки.

1.5.3.Здійснити аналіз результатів шляхом застосування статистичних критеріїв c2 – Пірсона та Колмогорова-Смірнова. Для цього:

-  побудувати гістограму розподілу частот виходячи із отриманих результатів та порівняти її із теоретичним розподілом, використовуючи критерій c2 ;

-  побудувати емпіричну функцію розподілу порівняти її із теоретичним розподілом, використовуючи критерій Колмогорова.

-  заповнити таблицю результатів статистичних досліджень у якій порівняти результати з еталонною вибіркою BBS.

1.5.4 Підготувати та оформити звіт з проведеної лабораторної роботи.

1.6 Порядок виконання роботи

1  Запустити додаток статистичного тестування NIST_STS.exe.

2  Виконати статистичні випробування вказаних викладачем ГВП. Для цього використати опис програмного забезпечення, що наведений у п. 1.4. цих вказівок.

3  З використання загальних результатів тестування, які містяться у файлі finalAnalysisReport зробити інтерпретацію результатів випробувань (Дивись приклад у додатку В)

4  З використанням результатів тестування, які містяться у файлі finalAnalysisReport, для вказаних викладачем статистичних тестів побудувати теоретичну та емпіричну гістограму частостей F_k потрапляння значень P_ij у кожний з k = 1, 2, …, 10 підінтервалів, на які розбитий інтервал [0, 1]  (Рис. 1.12)

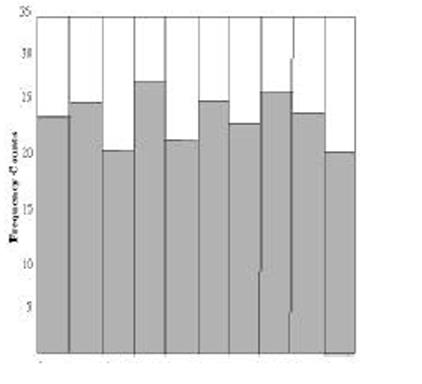
Рисунок 1.12­ – Зразок побудови гістограми

У відповідності до виразу

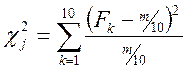
розрахувати значення c² та перевірити узгодженість теоретичного та емпіричного закону розподілу значень P_ij  при a=0,01 та a=0,05. Критичні значення для c² наведені Додатку А.

5  Перевірити узгодженість емпіричного та теоретичного закону розподілу значень P_ij для вказаних викладачем статистичних тестів за допомогою критерію Колмогорова-Смірнова. Для цього з використанням результатів тестування, що містяться у файлі result відповідного статистичного тесту, побудувати емпіричну функцію розподілу та теоретичну функцію розподілу для рівноймовірного закону. Обчисліть статистику Колмогорова-Смірнова (Додаток А). У якості критерію оцінки розбіжності теоретичної F_т(P_ij) те емпіричної F_е(P_ij) функції розподілу розглядається максимальне значення модулю різниці

.

Визначаємо значення

,

де m – число точок, за якими будувалася емпірична крива.

Знаючи b, за таблицею А.2 знайти ймовірність P(b). Якщо ця ймовірність мала, то гіпотеза про узгодженість законів відхиляється, і навпаки, якщо ймовірність велика, то гіпотеза приймається.

Перевірити узгодженість результатів, які буди отримані за допомогою критерію c² та критерію Колмогорова-Смірнова та зробити висновки.

Примітка: З метою спрощення виконання пунктів 7, 8 необхідно використовувати електроні таблиці Microsoft Excel.

1.7 Зміст звіту