Исследование криптографических свойств нелинейных узлов замены уменьшенных версий некоторых шифров

УДК 681.3.06

В.И. ДОЛГОВ, доктор техн. наук, А.А. КУЗНЕЦОВ, доктор. техн. наук,

И.В. ЛИСИЦКАЯ, канд. техн. наук, Р.В. СЕРГИЕНКО, А.Е. ОБУХОВ

ИССЛЕДОВАНИЕ КРИПТОГРАФИЧЕСКИХ СВОЙСТВ НЕЛИНЕЙНЫХ

УЗЛОВ ЗАМЕНЫ УМЕНЬШЕННЫХ ВЕРСИЙ НЕКОТОРЫХ ШИФРОВ

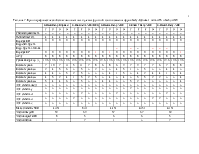
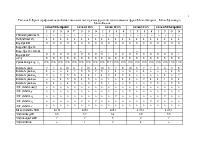
Рассматриваются S-блоки уменьшенных версий блочных симметричных шифров, представленных на проходящий в Украине конкурс на новый стандарт блочного симметричного шифрования. Приводятся результаты оценки свойств S-блоков конкурсных предложений и уменьшенных версий известных шифровBaby-Rijndael,  mini-AES и FOX. При этом используется две методики, - одна на основе математического аппарата линейной алгебры, а вторая  - на основе изучения комбинаторных свойств подстановочных конструкций. Делается вывод, что блоки нелинейных замен для рассмотренных мини версий блочных симметричных шифров имеют близкие криптографические показатели (за исключением mini-AES), и могут быть построены на основе отбора подстановок по критериям случайности с дополнительной фильтрацией по показателям максимально допустимых значений таблиц дифференциальных разностей и таблиц линейных аппроксимаций

1. Введение

Самые современные ключевые криптосистемы базируются на уже ставшей традиционной идее произведения шифров [1], которые представляют собой класс криптосистем, повторяющих сложную операцию, преобразующую плайнтекст в шифртекст. Каждое такое повторение (итерация) известно как цикл шифра [2]. Сложная (составная) операция, выполняющаяся в каждом цикле, является обычно комбинацией набора примитивных операций, таких как сдвиг, линейное преобразование, сложение по модулю и подстановку [3, 4]. В соответствующем сочетании эти преобразования должны реализовать концепцию построения таких шифров, которая, как известно, состоит в том, что комбинация перестановочных и подстановочных операций слабых в отдельности может привести к криптографически сильному нелинейному преобразованию, если оно применяется достаточное число раз. Подстановочные операции во многих шифрах выступают при этом как основной нелинейный элемент циклового преобразования. Поэтому значительные усилия исследователей направлены на изучение подходов к изучению свойств и построению подстановок с высокими криптографическими показателями.

Одним из популярных для описания и изучения свойств S-блоков стал математический аппарат линейной алгебры и, в частности, аппарат булевых функций. Этому направлению посвящено большое число работ [5-14 и мн. др.]. Если кратко характеризовать возможности этого подхода, то можно отметить, что его основой является представление
S-блока в виде композиции компонентных булевых функций с последующим изучением их свойств. К сегодняшнему дню уже наработан значительный набор подходов и широкий набор критериев оценки свойств компонентных функций. Вместе с тем, несмотря на очевидную результативность и убедительность этого подхода, он представляется все же достаточно сложным как для освоения, так и для практической реализации. С другой стороны, в свое время нами был предложен подход к построению (отбору) S-блоков [15-17], основанный на использовании показателей (критериев) случайности, следующих из общей математической теории  подстановок, имеющий на наш взгляд более простую реализационную и теоретическую основу. Правда, к этим критериям пришлось добавить дополнительные ограничения на максимально допустимые значения элементов таблиц дифференциальных разностей и линейных аппроксимаций, которые, однако, присутствуют и при использовании аппарата булевых функций. Возникло естественное желание попытаться установить связи между этими подходами, тем более, что в последнее время активизировалась работа по изучению свойств уменьшенных версий блочных симметричных шифров [18-21], облегчающих в рамках проходящего в Украине конкурса на новый стандарт блочного симметричного шифрования, позволяющих, по крайней мере, выполнить сравнение эффективности различных решений. В этих шифрах большие (байтовые) S-блоки заменяются уменьшенными S-блоками (при стремлении повторить в уменьшенной версии основные преобразования и структуру построения большого алгоритма), анализ которых существенно упрощается в связи с существенным сокращением необходимого объема вычислительных экспериментов. В этой работе выполняется сопоставление (сравнение) двух отмеченных подходов к анализу S-блоков, которое преследует цель: с одной стороны  - определить полезность привлечения для оценки и анализа криптографической стойкости S-блоков показателей их случайности (числа циклов, возрастаний и инверсий), а с другой, - найти подтверждения сохранению в уменьшенных моделях шифров (уменьшенных S-блоках) основных показателей (с учетом выполненного масштабирования) больших прототипов.

2. Конструкции S-блоков мини версий шифров, представленных на конкурс