Исследование криптографических свойств нелинейных узлов замены уменьшенных версий некоторых шифров, страница 5

В дальнейшем основное внимание будет сосредоточено на S-блоках размера . Такие S-блоки осуществляют отображение входного 4-битного вектора в выходной вектор такой же размерности, что на языке гомоморфизмов полей обозначает отображение . Математически такая подстановка представляется в виде матрицы из двух строк (перестановок без повторений) из 16-ти 4-х битных чисел каждая. Обычно рассматриваются подстановки представленные в каноническом виде (первая строка упорядочена по значениям 4-х битных входов), что в принципе позволяет рассматривать только вторую строку матрицы подстановок. В результате S-блок может быть представлен объединением четырех компонентных булевых функций ,  четырех переменных . Таблица 3 иллюстрирует четыре компонентные функции S-блока шифра Baby-Rijndael [28], повторяющего концепцию построения
S-блока шифра AES. Жирным шрифтом записана вторая строка матрицы-подстановки (третья строка в таблице 2).

Таблица 3. Таблицы истинности компонентных БФ S-блока шифра Baby-Rijndael

S	10	4	3	11	8	14	2	12	5	7	6	15	0	1	9	13
f1	0	0	1	1	0	0	0	0	1	1	0	1	0	1	1	1
f2	1	0	1	1	0	1	1	0	0	1	1	1	0	0	0	0
f 3	0	1	0	0	0	1	0	1	1	1	1	1	0	0	0	1
f 4	1	0	0	1	1	1	0	1	0	0	0	1	0	0	1	1

Приведем здесь основные пункты выполнения анализа свойств S-блоков, выполняемого с привлечением математического аппарата булевой алгебры. Воспользуемся методикой, изложенной в нашей работе [30], где рассмотрены свойства S-блоков шифра ГОСТ 28147-89. В качестве объекта исследований  будет выступать первая булева функция  f ₁  
S-блока из таблицы 3.

В [30] отмечено, что  одним из важнейших критериев эффективности булевой функции в криптографическом смысле является ее сбалансированность. Сбалансированные функции наиболее стойкие к прямым статистическим атакам. Определить, сбалансирована функция, или нет, можно прямым подсчетом единиц и нулей в ее таблице истинности. В данном случае функция имеет равное количество нулей и единиц: по восемь, поэтому она является сбалансированной.

Для определения других криптографических параметров функции (количества термов функции, количества термов, содержащих каждую переменную, алгебраической степени функции, алгебраической степени каждой переменной и др.) необходимо восстановить алгебраическую нормальную форму функции. Напомним, что алгебраической нормальной формой (АНФ) называется представление булевой функции в виде

.

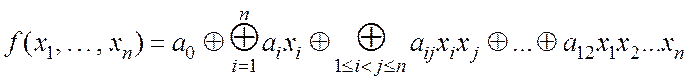Коэффициенты ,  при каждом терме в приведенном выражении (в рассматриваемом случае ) находят подстановкой в него значений переменных и фиксацией значения булевой функции в ее таблице истинности с последующим решением системы уравнений: 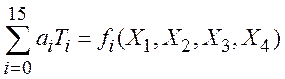, где  – i-тый одночлен АНФ функции. Соответствующие результаты расчетов для булевой функции  приведены в таблице 4.

Таблица 4. Значения коэффициентов при термах АНФ булевой функции

a0	a1	a2	a3	a4	a5	a6	а7	a8	a9	a10	a11	a12	a13	a14	a15
0	0	1	0	1	0	0	0	1	0	1	0	1	1	1	0

Найденные значения коэффициентов позволяют записать функцию  в необходимом виде: