Исследование криптографических свойств нелинейных узлов замены уменьшенных версий некоторых шифров, страница 7

При синтезе БФ, обеспечивающих высокую стойкость к дифференциальному, линейному и корреляционному криптоанализу, большое значение имеет автокорреляционная функция (АКФ) БФ. Автокорреляционная функция  для  определяется как

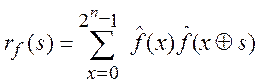
для всех . Здесь используется обозначение  = , с помощью которого обеспечивается преобразование значения {0, 1} функции  в значения {-1, 1}.

Говорят [9], что функция  f  удовлетворяет характеристике распространения m, если для значений s, заключенных в границы выполняется условие  . Автокорреляция  оценивает утечку (²просачивание²) информационного потока с входа на выход функции.

Аналогично, автокорреляция AC(f) функции f определяется как модуль наибольшего значения :

.

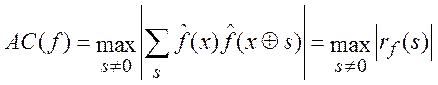Она была предложена Цзенгом и Цзангом как глобальная лавинная характеристика [13], поскольку включает все автокорреляции, не только соответствующие s с частными (низкими) весами Хэмминга.

  Результаты определения значения АКФ для всех возможных значений s для рассматриваемого примера приведены в таблице 6.

Таблица 6.  Расчеты значений АКФ для функции

s	АКФ	s	АКФ	s	АКФ
(1,0,0,0)	8	(1,1,0,0)	0	(1,1,1,0)	0
(0,1,0,0)	0	(1,0,1,0)	0	(1,1,0,1)	0
(0,0,1,0)	0	(1,0,0,1)	8	(1,0,1,1)	0
(0,0,0,1)	-8	(0,1,1,0)	-8	(0,1,1,1)	8
		(0,1,0,1)	0	(1,1,1,1)	-8
		(0,0,1,1)	0

Из таблицы следует, что автокорреляция функции  равна  8.

В аналогичном ракурсе определяется и другая глобальная характеристика - сумма квадратов различных автокорреляций, то есть

.

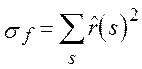3 Методика исследования криптографических свойств S-блоков с помощью критериев случайности.

Напомним основные положения второго из интересующих нас подходов к оценке криптографических свойств S-блоков. Следуя работе [15] применительно к подстановкам порядка n  введем понятие случайной (квазислучайной) подстановки, под которой понимается подстановка, удовлетворяющая трем критериям случайности, включающим выполнение следующих свойств:

Свойство 1. Число инверсий h_n  в подстановке степени n удовлетворяет условию

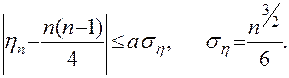
Свойство 2. Число циклов x_n  в подстановке степени n удовлетворяет условию

.

Свойство 3. Число возрастаний q_n в подстановке степени n удовлетворяет условию

.

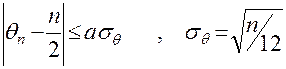В этих соотношениях a – параметр, выбираемый в значительной степени из субъективных соображений (по крайней мере, из условия, что множество допустимых подстановок будет не через чур уж ограниченным).

В этой же работе сделан вывод о возможности использования наиболее жестких из приведенных здесь условий отбора подходящих подстановок, а именно  значения . Для n = 16 это будут такие ограничения

1.

Установлено, что эти границы проходит около 50% всех подстановок, так что ²случайных² подстановок оказывается достаточно внушительное число. В итоге, методика отбора подстановок по критериям случайности сводится к проверке числа возрастаний, циклов и инверсий, реализуемых конкретным преобразованием. Например, для рассмотренного ранее S-блока шифра Baby-Rijndael результаты проверки свойств случайности позволили получить:  число инверсий в подстановке 59;  число циклов = 1;  число возрастаний  8.

В результате можно заключить, что рассмотренная подстановка является подстановкой случайного типа. Остается учесть дополнительные критерии отбора в отношении значений таблиц дифференциальных разностей и таблиц линейных аппроксимаций, которые будут обсуждены далее

4. Результаты расчетов криптографических свойств компонентных функций
S-блоков  и криптографических показателей S-блоков в целом