Исследование криптографических свойств нелинейных узлов замены уменьшенных версий некоторых шифров, страница 3

При  ® 0000 параметр  принимается равным значению . Если полубайт  также равен нулю (0000), то  ® 0011.

S-блоки шифра baby-Лабиринт. Как отмечает автор разработки [23], S-блок шифра Лабиринт выбран из множества предельно-нелинейных биективных преобразований. За основу и в этом случае взята конструкция Нюберг-Динга, т.е. преобразование аффинно-эквивалентное функции вычисления обратного элемента в поле GF(2⁸). Математически функция, определяющая преобразование S(x), осуществляемое S-блоком шифра Лабиринт, представляется в виде:

,

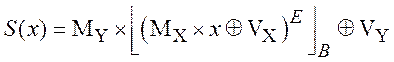где ; , ; B – некоторый базис над GF(2⁸), который определяется образующим (неприводимым) полиномом 8-й степени f_S(x); E – показатель степени; M_X, M_Y – квадратные невырожденные матрицы размера 8´8, с элементами из поля GF(2). В приведенном соотношении, для упрощения записи, вектора, участвующие в матричном умножении, рассматриваются как вектор–столбцы. Более полно с соображениями автора по выбору этого преобразования можно познакомиться в [23].

S-блок приведенный в спецификации к шифру был сформирован с использованием следующих параметров:

• Неприводимый (над GF(2)) полином, с помощью которого строится поле, есть   (в шестнадцатеричном представлении 0x1BD);

• Показатель степени ;

• Матрицы «входного» и «выходного» аффинных преобразований приведены ниже («вес» двоичных разрядов возрастает «сверху вниз» и «слева направо», т.е. элемент M[0,0], находящийся в верхнем левом углу, соответствует самому младшему разряду).

; ; ; .

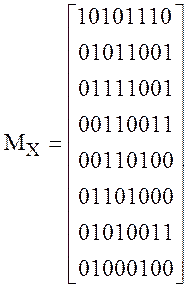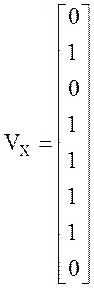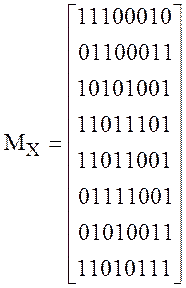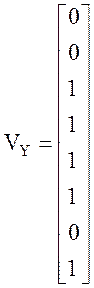Насколько оправдано такое усложнение процедуры, мы здесь обсуждать не будем. Заметим лишь, что авторы шифра Rijndael  постарались выбрать наиболее простую конструкцию, обеспечивающую необходимые показатели стойкости и высокое быстродействие. Они пошли даже на то, что взяли в своем шифре S-блоки одной и той же конструкции (повторяющиеся).

В уменьшенной модели шифра Лабиринт операции выполняются над полубайтами. Поэтому матрицы входного» и «выходного» аффинных преобразований были взяты размером , а конкретнее:

;     ; ; ,

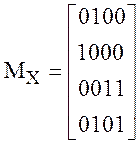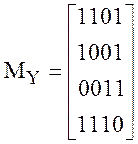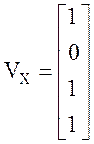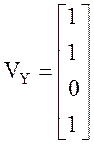т.е. строки (столбцы) рассматриваются как элементы векторного пространства, образуемому полем . Соответствующий неприводимый полином выбран вида , а параметр  Eвзят равным . Матричное представление подстановки вычисленной для этих параметров имеет вид:

.

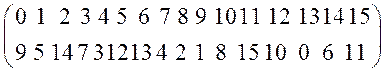Если изменить порядок отсчета разрядов векторов на обратный (в соответствии с указаниями разработчика), то можно прийти также к подстановке

.

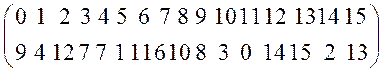S-блоки мини–Калина и мини-Мухомор.

            В шифре «Калина» [24] используется 8 различных подстановок “байт-в-байт”, причем для байтов одной строки текущего состояния шифра используется одна и та же подстановка. В описании шифра готовые таблицы подстановок приведены в приложении. Известно, что они построены с использованием конгруэнтного генератора ²случайных² чисел. Для шифра «Мухомор» [25] указывается, что таблицы подстановки совпадают с первыми 4-мя S-блоками алгоритма «Калина» Поэтому при построении уменьшенных моделей этих шифров предложено использовать или набор малых S-блоков (с разными или одинаковыми) параметрами  шифра baby-ADE, или малые S-блоки шифра Fox [29], обладающие, как утверждают авторы разработки, высокими дифференциальными и линейными характеристиками переходов. Мы в дальнейшем и сосредоточим свое внимание на более детальном изучении криптографических показателей отмеченного семейства малых S-блоков (подстановок 16-го порядка). В таблице 2 представлены построчно варианты подстановок 16-го порядка, которые будут исследованы далее. Для шифра «Лабиринт» приведены оба варианта представления разрядов входных и выходных векторов.

Таблица 2. S-блоки для уменьшенных версий шифров.