Исследование криптографических свойств нелинейных узлов замены уменьшенных версий некоторых шифров, страница 6

Из полученной АНФ функции простым подсчетом можно определить следующие криптографически важные свойства функции:

– количество термов в функции: ;

– количество термов в функции, содержащих определенную переменную:

2, , , .

– алгебраическую степень функции (нелинейный порядок функции), = 3;

– алгебраическую степень каждой переменной:  для всех i;

Аналогичным образом восстанавливается АНФ для остальных компонентных БФ:

,

,

.

Отмеченная группа показателей характеризует стойкость S-блока и шифра в целом к алгебраическим атакам, которые используют недостаточную сложность математического описания шифрующих преобразований.

Очередным важным криптографическим показателем булевой функции является ее нелинейность. Нелинейность функции численно определяется минимальным расстоянием Хемминга между данной функцией и всеми аффинными функциями векторного пространства , определяемого полем  [13, 14]:

,                   

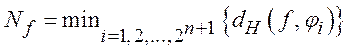где  аффинные функции над .

Для определения этого показателя строятся таблицы истинности всех возможных аффинных функций, и путем сопоставления этих таблиц с таблицами истинности булевой функции определяется значение минимального из расстояний Хемминга между данной функцией и всеми аффинными функциями. Для рассматриваемой булевой функции ,  оно равно 4, и, следовательно, значение нелинейности функции есть 4.

Существенным усилением свойства сбалансированности БФ является требование сбалансированности всех частных функций, полученных из исходной функции фиксированием любых ее k или менее переменных. Указанное требование позволяет обеспечить стойкость криптографических преобразований к статистическим атакам при фиксированных значениях битов на входе преобразования. Данное свойство связано с показателем корреляционной иммунности (КИ).

Говорят, что функция  обладает корреляционной иммунностью порядка k, если последовательность значений функции  статистически не зависит от подмножеств из k  координат-аргументов (значений входов) [13]:

.

Эквивалентное определение корреляционного иммунитета в терминах преобразования Уолша [13]: функция f над полем GF(2ⁿ) имеет корреляционный иммунитет порядка k, КИ(k), если ее преобразование Уолша (ПУ) удовлетворяет равенству F(w) = 0 для всех w Î V_n таких, что 1 £ W(w)£ k:

"w Î V_n          F(w) = 0           КИ(f) = k.

Напомним, что преобразование Уолша F(w) функции f над полем GF(2ⁿ) определяется как принимающая действительные значения функция [8]

F(w) = ×,

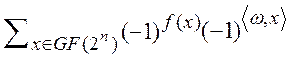где w Î V_n,  f(х), áw, xñ Î N , áw, xñ - скалярное произведение векторов w  и x
(áw, xñ= w₁Äx₁ Å … Å w_nÄx_n).

Корреляционно-эффективной является функция, для которой не менее чем для половины векторов веса 1≤ w ≤ q значения компонентов спектра ПУ равны 0.

Определим значения F(w) для всех возможных значений w: F(1,0,0,0) =
= () =  (4) = 1/4. Таким же образом вычисляем значения ПУ для других w. Результаты сведены в таблицу 5:

Таблица 5. Расчеты преобразований Уолша для булевой функции

ω	<x,ω>	F(w)	ω	<x,ω>	F(w)	ω	<x,ω>	F(w)
(1,0,0,0)	x1	4	(1,1,0,0)	х1 + х2	0	(1,1,1,0)	х1+х2+х3	-4
(0,1,0,0)	x2	4	(1,0,1,0)	х1 + х3	0	(1,1,0,1)	х1+х2+х4	0
(0,0,1,0)	x3	-4	(1,0,0,1)	х1 + х4	-4	(1,0,1,1)	х1+х3+х4	0
(0,0,0,1)	x4	8	(0,1,1,0)	х2 + х3	0	(0,1,1,1)	х2+х3+х4	8
			(0,1,0,1)	х2 + х4	4	(1,1,1,1)	х1+х2+х3+х4	4
			(0,0,1,1)	х3 + х4	-4

Полученные результаты свидетельствуют, что рассматриваемая функция не является корреляционно-иммунной, и даже не является корреляционно-эффективной, так как она имеет всего лишь 5 нулевых значений.