Программа как математический объект: Методические указания для самостоятельного изучения темы и выполнения РГР, страница 22

                         if  y ³ 0 then  y:= x - y else x := y- x;

                         if  x ³ 0 then  x:= x - y else y := y - x;

Данная программа в виде условных правил  имеет следующий вид:

(  x ³ 0 ® x:= x + y | истинно®y := y + x)

 (  y ³ 0 ® y:= x - y | истинно®x := y- x)

 (  x ³ 0 ® x:= x - y | истинно®y := y - x)

 Преобразуем эту программу в последовательность разделяющихся правил:

(  x ³ 0 ® x:= x + y | x < 0 ®y := y + x)

 (  y ³ 0 ® y:= x - y | y < 0®x := y- x)

(  x ³ 0 ® x:= x - y |   x < 0®y := y - x)

Рассмотрим  трассировочные таблицы только для двух путей (всего их восемь), остальные строятся аналогично.

Вариант 1.1.1

Фрагмент	Условие	x	y
x := x + y	x0 ³ 0	x1 =  x0 + y0	y1 = y0
y := x - y	y1  ³ 0	x2 = x1	y2 = x1 - y1
x := x - y	x2  ³ 0	x3 = x2 - y2	y3 = y2

Выводы условия: x₀ ³ 0 L y₁  ³ 0 L x₂  ³ 0 = x₀ ³ 0 L y₀  ³ 0 L x₁  ³ 0 =

 x₀ ³ 0 L y₀  ³ 0 L x₀ + y₀ ³ 0  = x₀ ³ 0 L y₀  ³ 0

Выводы присваивания: x₃ = x₂ - y₂ = x₁ - (x₁ -  y₁) = y₁ = y₀

                                        y₃ = x₁ -  y₁ = (x₀ + y₀ ) - y₀ = x₀

функция первой ветки: x₀ ³ 0 L y₀  ³ 0 ® x, y := y, x

Вариант 1.1.2

Фрагмент	Условие	x	y
x := x + y	x0 ³ 0	x1 =  x0 + y0	y1 = y0
y := x - y	y1  ³ 0	x2 = x1	y2 = x1 - y1
y := y - x	x2  < 0	x3 = x2	y3 = y2 -x2

Выводы условия: x₀ ³ 0 L y₁  ³ 0 L x₂  < 0 = x₀ ³ 0 L y₀  ³ 0 L x₁  < 0 =

 x₀ ³ 0 L y₀  ³ 0 L x₀ + y₀ < 0  = ложно

присваивание  не имеет смысла.

Объединяя  все варианты, получим функцию, которая определяется разделяющимся правилом, состоящим из шести частей:

( x ³ 0 L y ³ 0 ® x, y := y, x |

x = 0 L y <0 ® x, y := -y - x, y |

x > 0 L y < 0 ® x, y :=  - x, y+ x |

x < 0 L x + y ³ 0 ® x, y := x, - y - x |

x < 0 L x + y < 0  L y ³ 0® x, y := - x, y+ x |

x < 0 L y < 0 ® x, y := y, x )

Этому правилу соответствует диаграмма в плоскости x, y, показанная на рис.35. Данное разделяющееся правило преобразуем в следующее условное правило:

( x ³ 0 L y ³ 0 ® x, y := y, x |     

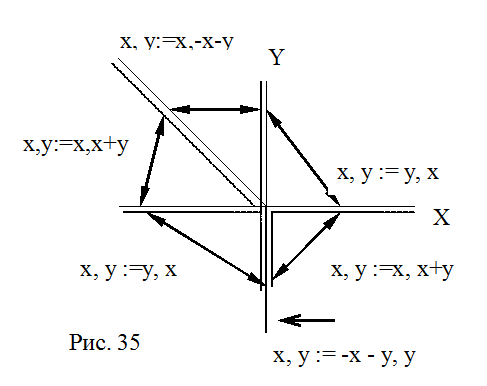
x = 0 ® x, y := -y - x, y |

x > 0 ® x, y :=  - x, y+ x |

 y < 0 ® x, y := y, x |

        x + y < 0 ® x, y := - x,  y+ x |

истинно ® x, y := x, - y - x )

4.4.6  Верификация программ типа for _ do.

 Программу типа  for _ doможно рассматривать как сокращённую форму записи обобщённой последовательной  программы. Например, программа типа

Q = fori : Î 1 to6 by 2dos := max ( i, s + i ) od является сокращённой записью обобщённой последовательности

R = s := max ( 1, s + 1); s := max ( 3, s + 3); s := max ( 5, s + 5);

В этом случае программная функция программ Q и R легко определяется по трассировочной таблице:

Фрагмент	s
s := max (1, s +1)	s1 := max (1, s0 +1)
s := max (3, s +3)	s2 := max (3, s1 +3)
s := max (5, s +5)	s3 := max (5, s2 +5)

с выводом  s₃ = s := max (5, s ₂+5) = max (5,  max (3, s₁ +3) +5) =

 max (8, s₁ +8)  = s := max (8,  max (1, s₀ +1) +8) = s := max (9, s₀ +9) и функцией программы    s := s := max (9, s +9).

Однако, если программа типа for _ do дана в общём  виде с параметром n, определяющим размерность цикла, например:

P_n = fori : Î 1 ton by 2dos := max ( i, s + i ) od, то в этом случае для доказательства правильности программы используется метод математической индукции. При использовании метода математической индукции возможны две стратегии в определении программной функции for _ do, основанные на выборе переменной, по которой проводится индукция. В качестве такой переменной можно выбрать целочисленную переменную из описания списка for _ do. При другом варианте ею может быть размер самого списка for _ do. В любом случае используется классическая схема математической индукции: