Для функций действительны операции над множествами, если они не нарушают правило единственности значений функции. Так, если f и g - функции, то f Çg, f - g также являются функциями, но f È g не может быть функцией, так как (x, y) Î f, (x, z) Î g не удовлетворяет требованию единственности значения функции для случая y ¹z.
Если f и g- функции, то {(x, y) | y = f (g (x))} называется композицией ( суперпозицией) функций g и f и обозначается как f ° g.
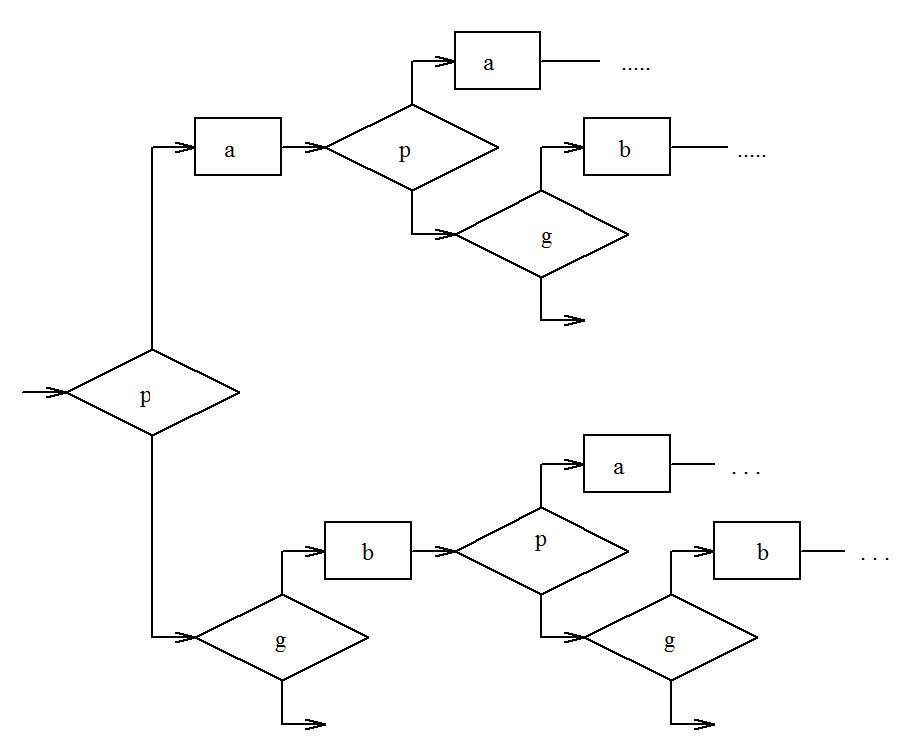
Рис. 10
Если функция f рефлексивна, то она называется тождественной функцией при f(x) = x для каждого xÎD(f).
Если существует функция f т такая, что f т(f (x)) = f( f т(x)) = x, то f т называется обратной функцией от f.
Если область значения функции f - это одноэлементное множество, то функция является константой ; если же область значения функции является множество {истина , ложь},она называется предикатной функцией ( предикат). Предикатная функция часто задаётся условиями из области определения. Например, предикат, заданный в форме
p = {( x, истина ) | x ³ 0} È {( x, ложь) | x < 0}является обозначением того, что x ³0, т.е. выделяется область, в которой предикат p принимает значения истина.
Предикатные функции можно использовать для описания других функций. Например,
f = {(x,y) | (x ³ 0 ® y = 3 | x < 0 ® y =4)}
В общем случае правило для функции можно задать в форме условного правила вида ( предикат ® правило), разделённых вертикальной чертой:
(p1 ® r1 | p2 ® r2 | ... | pk ® rk )
Такое условное правило означает следующее: предикаты p1, p2, ... pk вычисляются последовательно слева направо и будет выполнено правило
ri , если соответствующий предикат pi первым принял значение истина ; если ни один из предикатов не принимает значение истина, то правило считается неопределённым. Другими словами данное выражение следует рассматривать как схематической записью оператора CASE или схему вложенных операторов IF_THEN_ELSE. Если pk является предикатом с постоянным значением истина, а все предшествующие предикаты принимают значение ложь, то в этом случае всегда выполняется правило rk; например,
f = {(x, y) | xÎ D,( x делится на 2 ® y = x/2 |
x делится на 3 ® y = x/3 |
истина ® y = x)}
Правило в круглых скобках эквивалентно записи:
IF x делится на 2 THEN y = x/2 ELSE
IF x делится на 3 THEN y = x/3 ELSE y = x
3.2.2 Рекурсивные функции
Рекурсивная функция - это функция, использующая в своём определение саму себя. Рекурсивные правила могут быть использованы для описания сложных функций, когда эти функции трудно определить иначе. Например, пусть G – граф, который является моделью железнодорожной сети, связывающей несколько городов, а C(x, y) - предикат, определяющий условие существования железнодорожной связи между любыми двумя городами:
G = {(x, y) | поезд идёт из x и y}
С(x, y) = путь из x в y имеется
Тогда предикатная функции С может быть определена рекурсивно так:
C = {((x, y), w) | (x и y - города), w= C(x, y)}, где
С(x, y) = ((x, y) Î G ® w = истина | $z ((x, z)ÎG L C(z, y)) ® w = истина | истина ® w = ложь )
Это означает, что C(x, y) принимает значение истина в том случае, если либо есть прямая связь из x в y, либо возможно её установить через некоторый город z, в противном случае C(x, y) принимает значение ложь.
Заметим, что любое условное правило, определяющее функцию, можно записать как логическое высказывание
C(x, y) =((x, y)ÎG) V ($z ((x, z)ÎG L C(z, y))).
3.2.3 Функция и операция присваивания
Проектировануя программы, мы будем рассматривать оператор присваивания, как функцию, которая управляет изменением состояниями данных, содержащихся в проектируемой программе. Область определения функции соответствует исходному состоянию данных, которые с помощью оператора присваивания преобразуются в результирующее состояние данных. Например, в программе с полем данных x, y, z присваивание x := y будет соответствовать функции присваивания, т.е. множеству упорядоченных пар, которые можно представить так :
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.