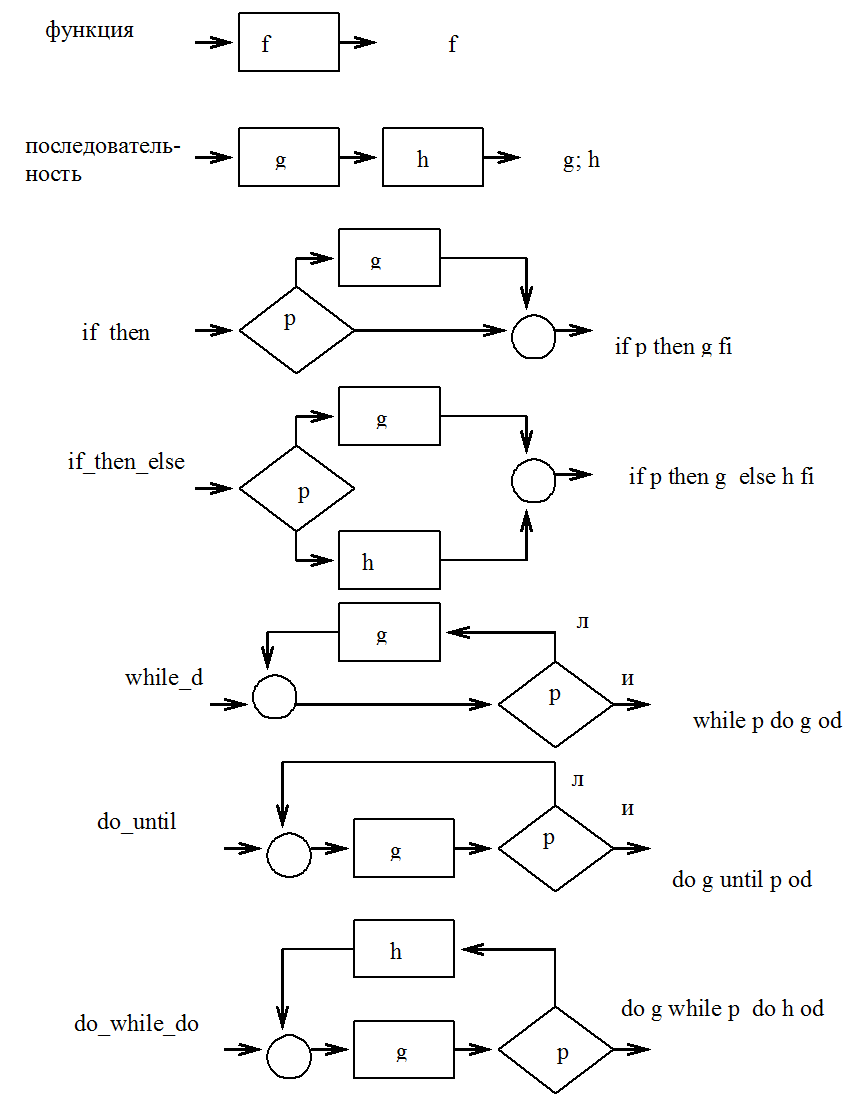
Элементарной программой называется простая программа, не содержащая простых подпрограмм более чем из одного узла. Примеры элементарных программ, соответствующие управляющим структурам языка PDL (рис. 20).
3.3.2 Составные программы
Если функциональный узел элементарной программы заменить другой элементарной программой, то в результате получится новая простая программа, которую будем называть составной программой.
Составные программы могут быть определены как программы произвольного размера, но ограниченной сложности, так как элементарные программы выбираются из фиксированного базисного множества. Каждое базисное множество элементарных программ позволяет создавать конкретный класс составных программ, являющихся подмножеством всех возможных простых программ. Например, множество {последовательность, if_then_else} даёт возможность построить класс программ без циклов, а множество {if_then_else, while_do} определяет класс программ, деревья выполнения которых содержат на любом пути не более одного функционального узла ( возможно повторяющихся).
Структурной программой называется составная программа, сформированная на основе фиксированного базисного множества элементарных программ.
3.3.3 Теорема о структурировании
.
Теорема о структурировании. Любая простая программа функционально эквивалентна структурированной программе, составленной из элементов базисного множества {последовательность, if_then_else, while_do} с использованием
функций
и предикатов исходной программы, а также операций присваивания и тестов над
дополнительной переменной, называемой счётчиком.
Доказательство. 1) алгоритм построение структурированной программы по данной простой, не структурированной программе:
а) пронумеровать все узлы схемы, при этом порядок обхода произвольный;
б) пронумеровать все дуги схемы следующим образом: выходной дуге схемы припишем номер 0, всем остальным дугам присвоим номер вершины, в которую данная дуга входит.
в) для каждого функционального узла, имеющего номер i и выходную дугу с номером j, составим новую простую последовательную программу Gi с номером входной дуги i;
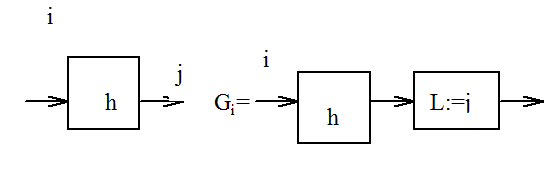
г) для каждого предикатного узла с номером t составим новую простую программу
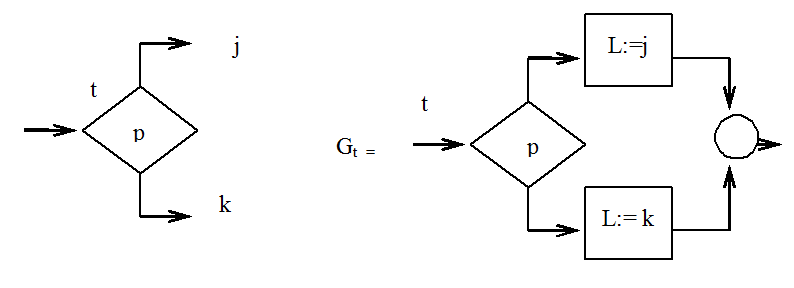
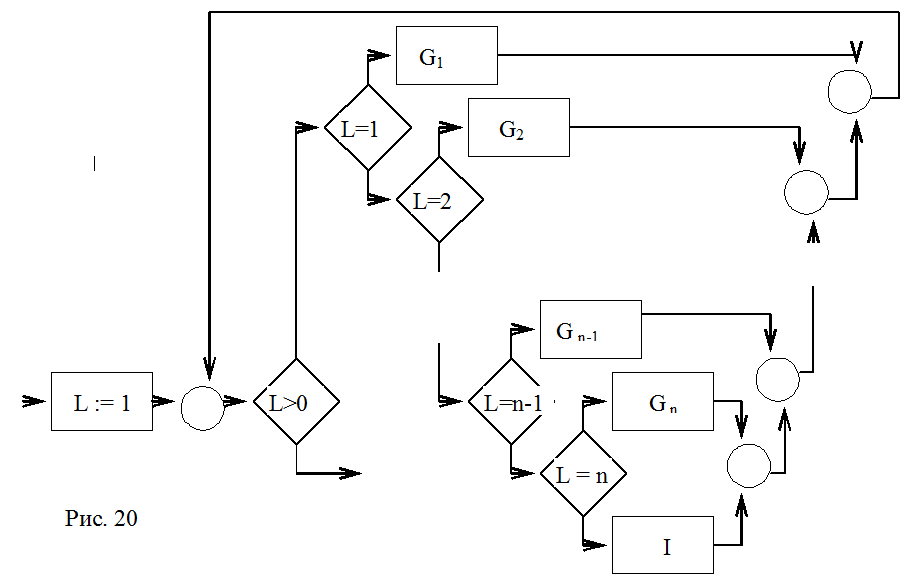
д) теперь построим программу типа while _ do с do - частью в виде вложенной структуры if _ then _ else, проверяющей значения L от 1 до n. Каждая выходная линия if _ then _ else соответствующая значению истина, соединяется с узлом Gi , являющимся функциональным или предикатным узлом исходной программы.
Схема структурированной программы и структурированная программа показаны на рис. 20 ( I на схеме обозначат тождественную функцию).
F = L := 1; whileL>0
doifL =1
thenG 1
elseifL =2
then G 2
. . .
else if L =n-1
then G n-1
else if L =n
then G n else I fi fi . . . fi fi od
Такая структурированная схема называется помеченной структурированной схемой. Ясно, что какой бы ни была исходная программа, программа F ей функционально эквивалентна. Более того, программа F является структурированной программой, сгенерированной из элементов базисного множества {последовательность, if _then _ else, while _ do}. Таким образом, доказательство закончено.
Приведённое выше конструктивное доказательство позволяет преобразовать произвольную блок - схему в программу, составленную из элементарных программ базисного множества {последовательность, if _then _ else, while _ do}. Рассмотрим, например схему, изображённую на рис. 21.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.