Программа как математический объект: Методические указания для самостоятельного изучения темы и выполнения РГР, страница 13

 

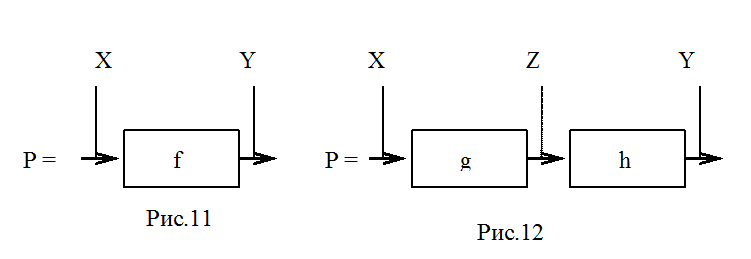
Например, программная функция для схемы - программы (рис.13) с соответствующей  Е - схемой (рис.14)  описывается следующим образом:

Первый путь описывается: а) высказыванием  p(f(X)) L  Y= g(f(f(X)))

                                              б) условным правилом  p·f(X) ® Y = g · f ·f (X)

· - символ обозначает композицию (суперпозицию функций), используется для сокращения записи  выражений, так  как можно опускать лишние скобки.

Аналогично описываются две других ветки:

Второй путь  - p(f(X)) L p( g ( f(X)))L Y= g( g(f(X))) или

                          p ·f(X) L p· g · f(X)® Y= g· g ·f(X)

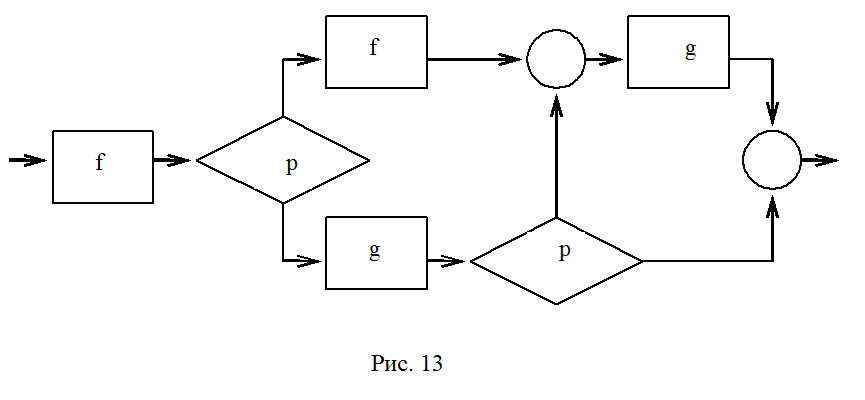
Третий путь - p(f(X)) L p( g ( f(X)))L Y= g(f(X)) или

                          p ·f(X) L p· g · f(X)® Y= g ·f(X)

Полностью программная функция данной схемы  описывается следующим образом:

[P] = {(X, Y) | p(f(X)) L  Y= g(f(f(X))) | p(f(X)) L p( g ( f(X)))L Y= g( g(f(X))) | p(f(X)) L p( g ( f(X)))L Y= g(f(X))} -  объединение высказываний

[P] = {(X, Y) | p·f(X) ® Y = g · f ·f (X) | p ·f(X) L p· g · f(X)® Y= g· g ·f(X) | p ·f(X) L p· g · f(X)® Y= g ·f(X)} - объединение условных правил.

      

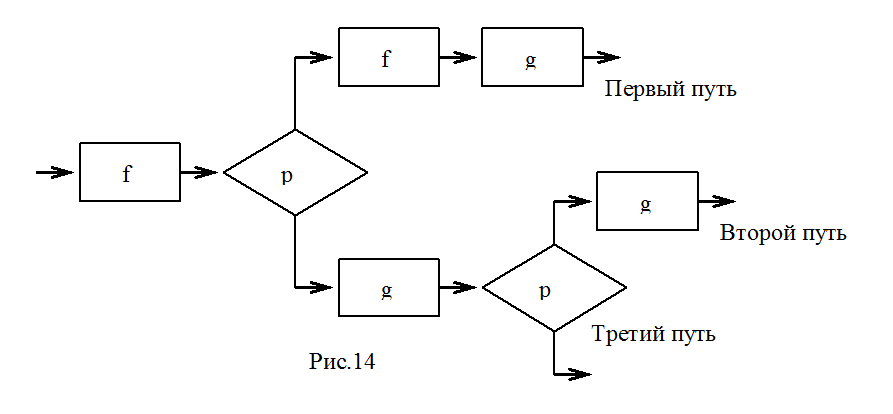
    Программная функция  для циклических схем описывается системой  рекурсивных равенств, которые определяются по соответствующей Е - схеме. Рассмотрим основные правила описания программной функции циклической  схемы - программы на примере показанном на ( рис.15).

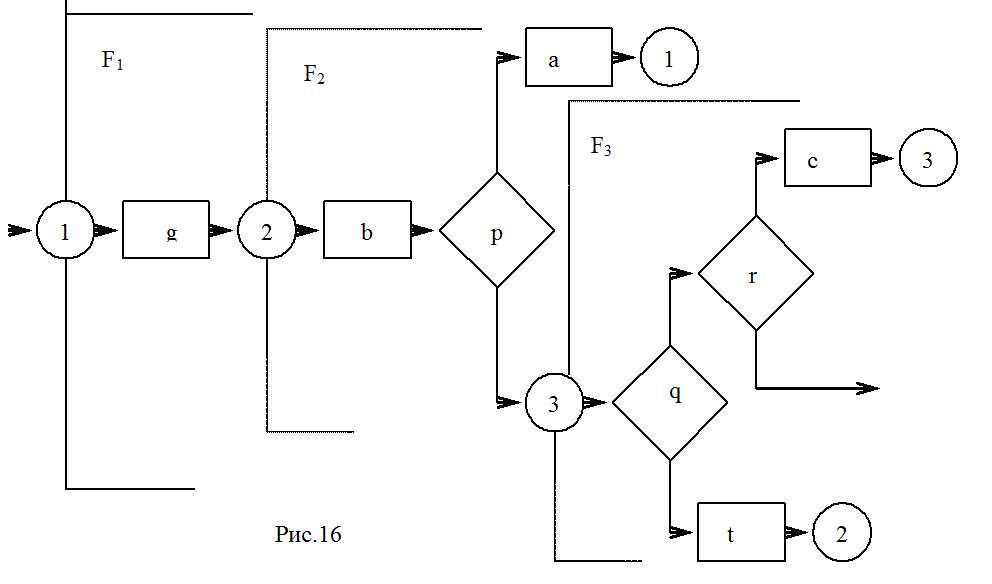
Во - первых, постройте Е - схему(рис .16). Количество путей, оканчивающихся узлами слияния, определят количество уравнений в системе, определяющей функцию программы.

Во - вторых, по первым вхождениям узлов слияния разделите схему на подсхемы. Каждую подсхему  обозначьте f_i , где i номер соответствующего узла слияния.(рис.16)

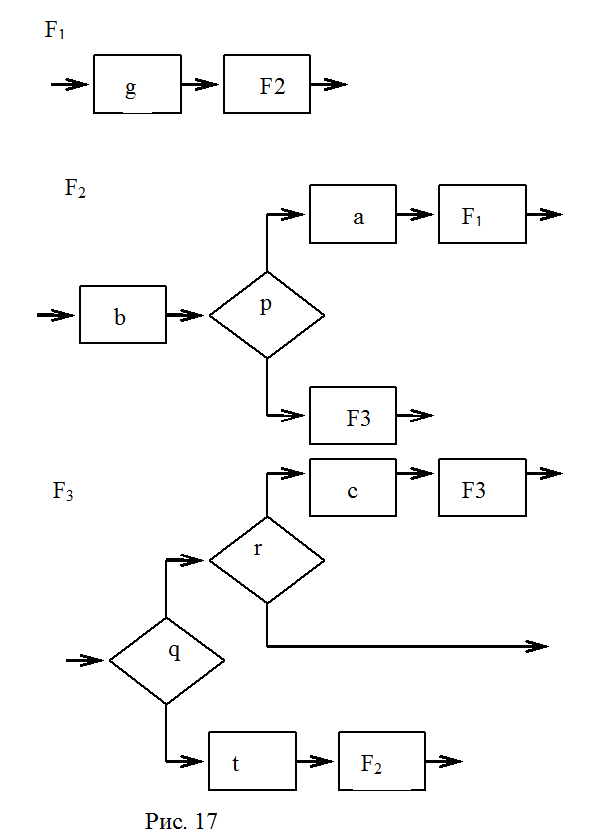
В - третьих, в каждой подсхеме узлы слияния заменить на функциональный узел с именем f_i , где i - номер, заменяемого узла слияния. (рис. 17)

В - четвёртых, описать функцию каждой подсхемы (рис. 17). Функция описывается так же как функция   ациклических схем.

f₁  = {(X, Y) | (Y = f₂·g(X))}

f₂  ={(X, Y) |  (p·b(X) ® Y= f₁·a·b(X) |

                     Ø p·b(X) ® Y= f₃·b(X))  }

f₃ = {(X,Y) | (q(X) L r(X) ® Y= f₃·c(X) |

                     q(X) L  Ør(X) ® Y= X |

                   Ø q(X) ® Y= f₂·t(X))}

Если эта система равенств может быть решена, то программная функция программы P есть [P] = f₁.

3.2.5 Эквивалентность программ

В теории программировании определяется два  вида эквивалентности: эквивалентность по выполнению и функциональная эквивалентность. Если две программы имеют тождественные деревья, то они эквивалентны по выполнению, если же они имеют тождественные программные функции,  то они функционально эквивалентны. Эквивалентность по выполнению предполагает функциональную эквивалентность, но не наоборот.

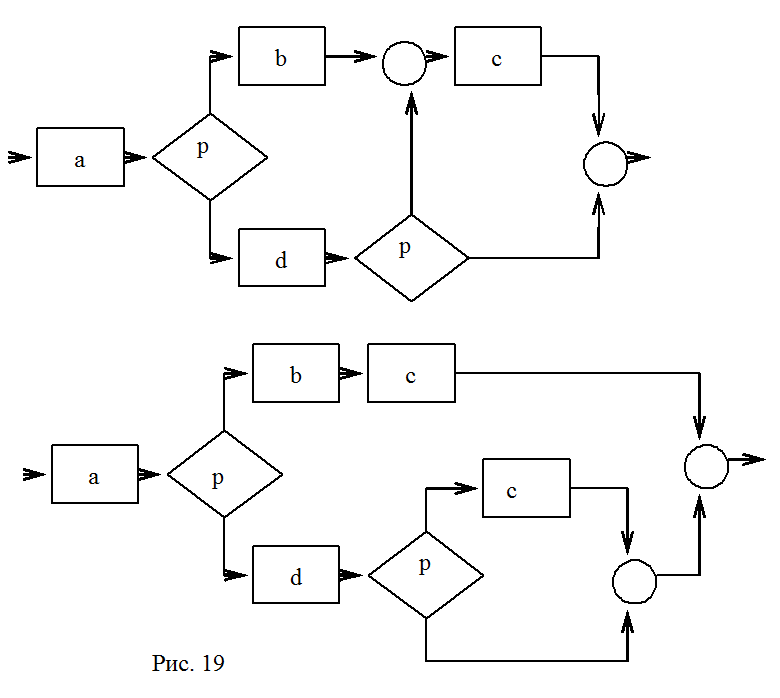
 Для определения эквивалентности по выполнению не обязательно строить деревья выполнения. Можно по любой схеме построить регулярное выражение. Если регулярные выражения совпадают, то схемы эквивалентны по выплнению. Например, на рис. 19 приведён пример схем эквивалентных по выполнению, так как первая схема описывается регулярным выражением – abc + adc, и вторая схема – abc +adc. Ниже приведены программы эквивалентные функционально, но не эквивалентные по выполнению.

P = while y >0 do x:= x - 1; y:=  y - 1 od;

 [P] ={( x, y) | (y > 0 ®  x, y = x - y, 0 | y £ 0 ®  x, y = x , y)}

S = if y  >0 then x:= x - 1; y:= y - 1; x, y := x- y, 0 if; 

[S] = {( x, y) | (y > 0 ®  x, y = x - y, 0 | y £ 0 ®  x, y = x , y)}

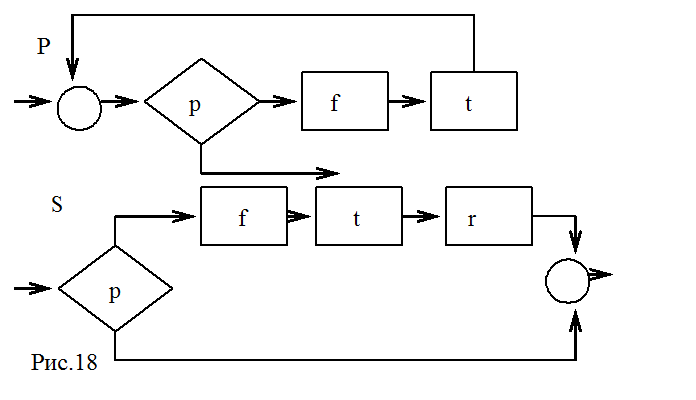
Если выражение y >  0 обозначить p,  операторы x:= x  - 1;y:= y - 1  - соответственно f и t, а оператор x, y: = x -  y, 0 - r, то схемы программ P и S приведены на рис. 18.

Хорошо видно,

что деревья для этих схем будут различны. Регулярное выражение тоже будут различны, для программы Р – (ft)*, а  для программы S – ftr, и следовательно, программы не эквиваленты по выполнению.

           3.3 Программные структуры

       3.3.1 Элементарные программы