Программа как математический объект: Методические указания для самостоятельного изучения темы и выполнения РГР, страница 15

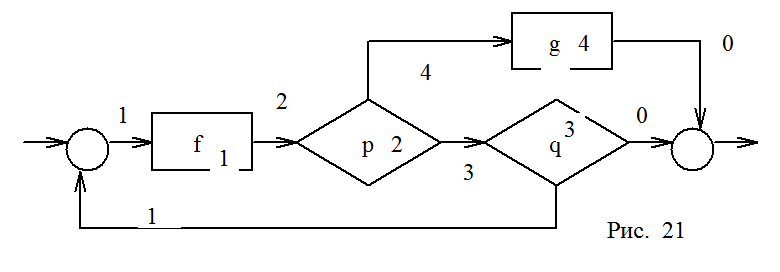
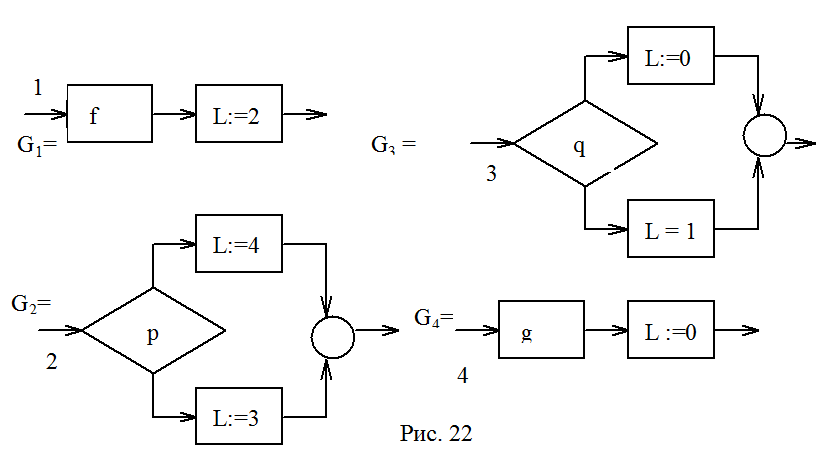
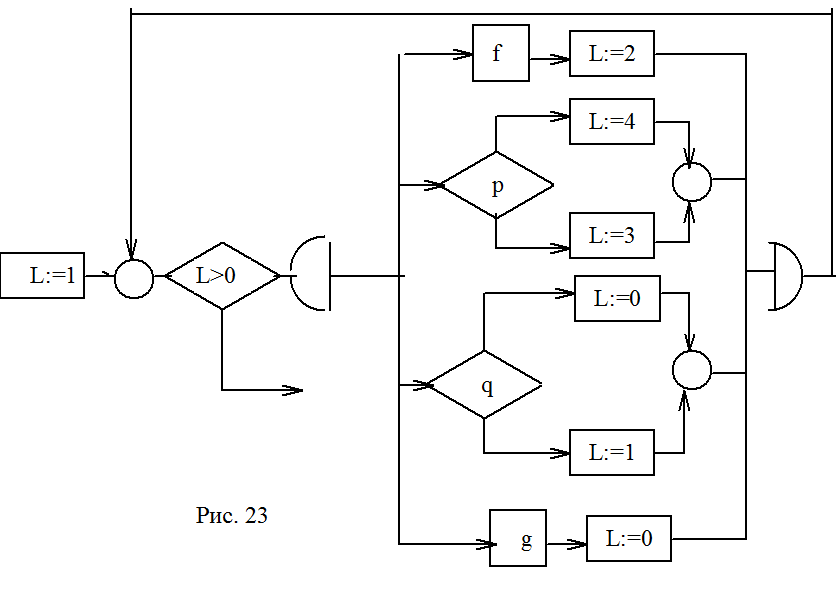
В схеме на рис. 21 пронумерованы узлы и дуги. Согласно алгоритму построения получим новые программы:  последовательности и программы if _ then _ else (рис. 22), которые могут быть собраны в структурированную программу, показанную на рис. 23. В этой схеме с вложенные if заменены на структуру case

               В

L := 1; while L>0   do                               L := 1; while L>0   do case L

 if  L=1       then   f ; L = 2;                                    part( L = 1) f ; L: = 2;

      else    if         L =2                                                part( L = 2)

    then   if p then L := 4 else L := 3 fi                   if p then L := 4 else L := 3  fi              

                                        else if          L = 3                            part( L = 3)

    then if q then L := 0 else L := 1 fi                      if q then L := 0 else L := 1 fi

                                        else if         L =4                               part( L = 3)

   then    g; L := 0  else I fi fi  fi fi  od                        g; L := 0 esac od

.

3.3.4.Рекурсивные структурированные программ

Помеченная структурированная программа это всего лишь конструктивное доказательство теоремы и данная структура мало пригодна для практического использования. Попытаемся преобразовать программу к первоначальному виду, сохраняя свойство структурированности. Для этого исключим излишние присваивания и проверки счётчика L. Ниже приведён алгоритм преобразования помеченной структурированной схемы в рекурсивную, структурированную схему с сохранением функциональной эквивалентности.

Алгоритм: для каждого j>0 заменить все присваивания L:= j соответствующей программой  G_j. ( Заметим, что для L = 1 установка L:= 1, предшествующая while _ do, должна быть заменена на  G₁ так же, как и для каждого другого вхождения L := 1.) Поскольку значение j теперь никогда не будет присвоено L, проверку L = j можно убрать из  структуры,  не нарушая функциональной целостности исходной программы. Один шаг такого преобразования приводит к новой последовательности подпрограмм  G^¢₁, G^¢₂, G^¢₃,..., G^¢_n-1, где функции g^¢ могут быть при необходимости перенумерованы.

 Процесс повторяется до тех пор, пока:

1) все присваивания  L, кроме L:= 0, не будут исключены;

2)  либо каждая оставшаяся программа G^¢_i  не будет содержать  присваивания L:= i ( прямая рекурсия), либо  не будет содержать  присваивания L := j, а программа G^¢_j  будет содержать  присваивания L := i (косвенная рекурсия ).

 

Если программа ациклическая, то на каждом пути появятся присваивания L:=0; следовательно, счётчик L и цикл while могут быть также исключены. То, что остаётся, является составной структурированной программой, эффективной по выполнению и функционально эквивалентной исходной программе.

Например, построим рекурсивную структурированную программу для помеченной структурированной схемы из параграфа 3.3.3.

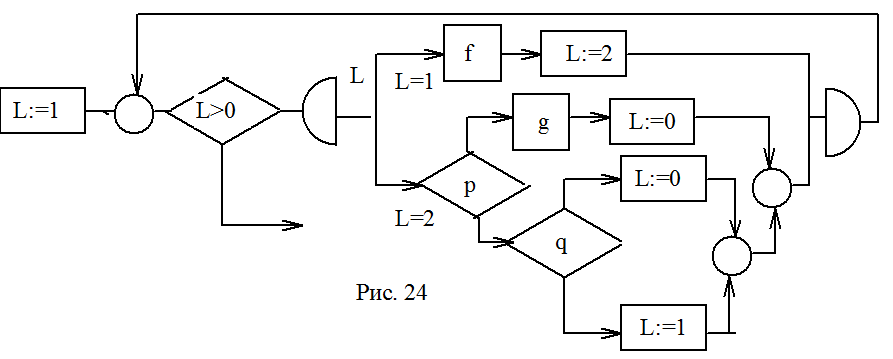
На первом этапе преобразования убрали значение счётчика L=4 и L=3, вставив на их место соответствующие подпрограммы (рис. 24). На втором этапе преобразования  заменим L:=  2 на подпрограмму G^¢₂. Поскольку, в схеме осталось единственное значение счётчика L = 1,то  эту проверку можно убрать. Результирующая структурированная программа показана на рис. 25.

Если проанализировать схему исходной программы (рис.21), почему она нее является структурированной, то хорошо видно, что элементарная подпрограмма типа do _until имеет  два выхода. В практике  программирования известно, что одним из решений такого рода ситуаций является использование дополнительной  переменой с двумя состояниями, которая управляет окончанием цикла наравне с основным правилом. Как видим  в результате формальных преобразований мы получили такой же результат, счётчик L имеет два состояния { 0,1} и играет роль дополнительной переменной, управляющей окончанием цикла.