x > 0 L x £ y ® z := y |
x£ 0 L y > 0 Lx < y ® z := x |
x£ 0 L y > 0 L x ³ y ® z := y)
В последнем правиле условие противоречиво ( тождественно ложно), поэтому это правило исключить из разделяющихся правил;
5) Оставшиеся правила можно пояснить с помощью диаграммы на плоскости x, y, как показано на рис. 32
6) обратное преобразование в условное правило,
записанное без использования операций max и min.
4.4.4 Сравнение условных правил
При сравнении двух условных правил в процессе верификации более удобна разделяющаяся форма этих условных правил. Предположим, разделяющиеся правила (p1 ® r1 | p2 ® r2 | p3 ® r3 ) и (q1 ® s1 | q2 ® s2 ) сравниваются с целью определения полной корректности. В этом случае необходимо и достаточно, чтобы правила 1) задавали идентичные области определения и 2) совпадали при каждой парной конъюнкции предикатов правил, т. е. Должны выполняться соотношения:
p1 V p2 V p3 = q1 V q2 (идентичные области определения) и
(p1 Lq1 ® r1) = (p1 Lq1 ® s1)
(p1 Lq2 ® r1) = (p1 Lq2 ® s2)
(p2 Lq1 ® r2) = (p2 Lq1 ® s1)
(p2 Lq2 ® r2) = (p2 Lq2 ® s2)
(p3 Lq1 ® r3) = (p3 Lq1 ® s1)
(p3 Lq2 ® r3) = (p3 Lq2 ® s2) (сравнение каждой парной конъюнкции).
Например, сравним два условных правила:
(x ³ 0 Ly ³ 0 ® x:= x - y | x ³ 0 L x + y ³ 0 ® x:= x + y) и
(x + y ³ 0 Ly £ 0 ® x:= x + y | x ³ 0 L x + y > 0 ® x:= x - y)
1) разделение условий : (преобразование второго предиката первого правила можно записать как
Ø(x ³ 0 L y ³ 0 ) L x ³ 0 L x + y ³ 0 = ( x < 0 V y < 0) L x ³ 0 L x + y ³ 0 =
y < 0 L x ³ 0 L x + y ³ 0;
второй предикат второго правила приводится к следующему виду:
Ø ( x + y ³ 0 L y £ 0) L x + y > 0 L x ³ 0 = (x + y < 0 V y > 0) L x + y > 0 L x ³ 0
= y > 0 L x + y > 0 L x ³ 0.
2) исходные правила в разделяющейся форме выглядят так:
(x ³ 0 L y ³ 0 ® x := x - y | y < 0 L x ³ 0 L x + y ³ 0® x := x+ y)
(x + y ³ 0 L y £ 0 ® x := x + y | y > 0 L x + y > 0 L x ³ 0 ® x := x - y)
3) проверка равенства областей определения:
верно ли, что (x ³ 0 L y ³ 0) V (y < 0 L x ³ 0 L x + y ³ 0) =
(x + y ³ 0 L y £ 0) V (y > 0 L x + y > 0 L x ³ 0) ?
О равенстве областей определения можно судить по диаграмме (рис. 33)
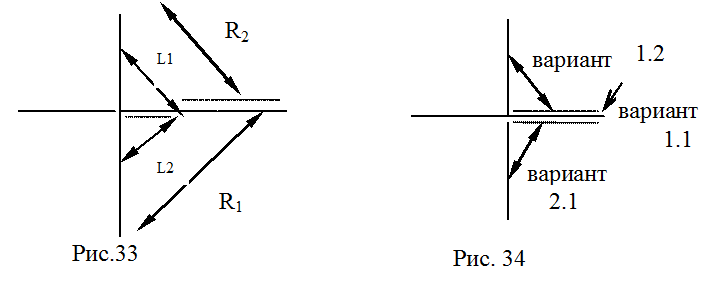
L1, L2 - область определения первого условного правила, а R1, R2 - область определения второго условного правила.
4) Проверка равенства правил:
вариант 1.1 (x ³ 0 L y ³ 0 )L (x + y ³ 0 L y £ 0) (p1 Lq1)
верно ли, что x := x - y = x := x + y ? (r1 = s1)
поскольку y ³ 0 и y £ 0 , то данное выражение истинно при y =0, следовательно x := x - y = x := x + y равенство истинно.
вариант 1.2 ( x ³ 0 L y ³ 0 )L (y > 0 L x + y > 0 L x ³ 0) (p1 Lq2)
верно ли, что x := x - y = x := x - y ? (r1 = s2) равенство очевидно
вариант 2.1 (y < 0 L x ³ 0 L x + y ³ 0) L( x + y ³ 0 L y £ 0) (p2Lq1)
верно ли, что x := x + y = x := x + y ? (r2 = s1) равенство очевидно.
вариант 2.1 (y < 0 L x ³ 0 L x + y ³ 0) L (y > 0 L x + y > 0 L x ³ 0) (p2 Lq2)
верно ли, что x := x + y = x := x - y ? (r2 = s2)
Так как выражение (p2 Lq2) тождественно ложно ( y < 0 L y> 0), данное равенство можно не рассматривать. Диаграмма, показанная на рис.34 , соответствует трём определённым выше случаям.
4.4.5 Трассировочные таблицы для последовательностей условных правил
Для определения программной функции программы, состоящей из последовательности условных правил, необходимо описать все возможные пути вычисления в этой программе. Это делается так же, как и при описании функции схемы - программы без циклов. ( см. 3.2.4 рис. 13 ). Отдельно описывается каждый путь в Е - схеме и для него составляется трассировочная таблица, которая отличается от трассировочной таблицы для обычных последовательностей лишь тем, что добавляется столбец условий. Рассматривая реальную программу из последовательности условных правил, можно не строить Е - схему, а достаточно преобразовать программу в последовательность разделяющихся правил. Например, if x ³ 0 then x:= x + y else y:= y + x;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.