Программа как математический объект: Методические указания для самостоятельного изучения темы и выполнения РГР, страница 16

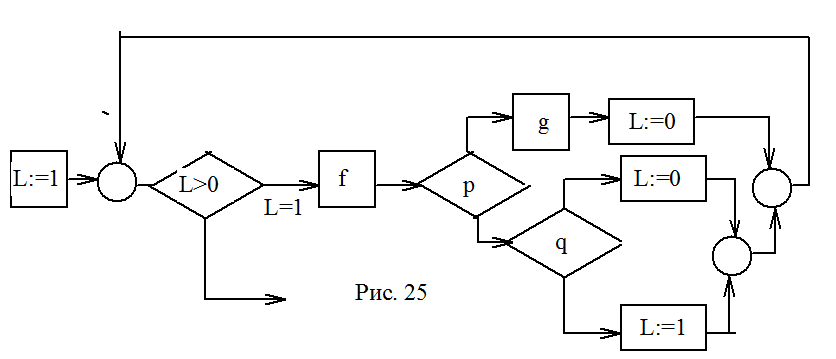
     3.3.5 Алгебра структурированных программ

Если P - простая подпрограмма программы Q, и P замещается на P^¢, то получим программу Q^¢. При этом ,  [P] = [P^¢] ® [Q] = [Q^¢] - аксиома замещения.

Два важных следствия:

1) значения истинности любого высказывания, включающего[P], не зависит от замещения P на P^¢, при условии равенства их функций;

 2) элементарные программы могут быть абстрагированы в функциональные узлы, а функциональные узлы могут быть представлены в виде элементарных программ независимо от их окружения в общей управляющей структуре.

Расширение и абстрагирование есть по существу алгебраические операции над структурированными программами.

Таким образом, алгебра структурированных программ позволяет рассматривать структурированную программу любой сложности как составное программное выражение над меньшими структурированными программами, а любые сложные программные выражения - как одно выражение, если это, конечно, удобно. Это свойство структурированных прошграмм позволяет описывать их регулярными выражениями.

3.3.6 Анализ элементарных программ

Работа по преобразованию произвольных программ в структурированные программы может быть упрощена путём выделения тех частей программы, которые уже структурированы. Для этого достаточно в исходной схеме выделить все элементарные подпрограммы и заменить каждую новым функциональным узлом. В результате получим  упрощённую схему функционально эквивалентную исходной программе. Далее применим данное преобразование к промежуточной схеме и получим ещё более простую программу и так далее.

Процесс  выделения и замещения элементарных программ новыми функциональными узлами, продолжающийся до тех пор, пока не останется ни одной не замещённой элементарной программы, называется анализом элементарных программ. При этом если программа была структурирована, она свернётся в один функциональный  узел. В противном случае мы получим схему, которую будем называть непоименованный блок. Непоименованный блок, как любая простая программа, должен иметь один вход и один выход.

Теперь для того чтобы структурировать исходную программу, достаточно структурировать непоименованный блок, а после раскрыть все свёрнутые на этапе анализа  функциональные узлы.  Пример анализа приведён ниже:

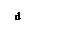
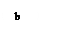
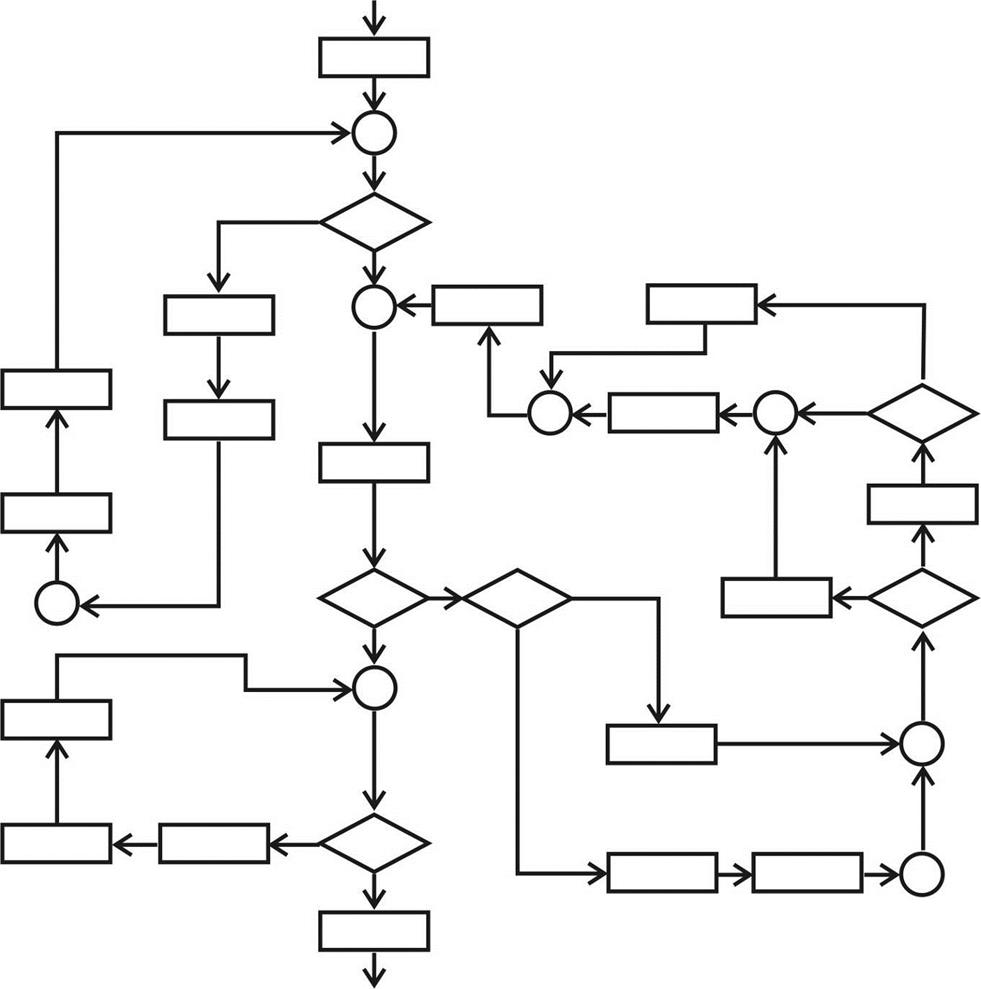
Рис. 26

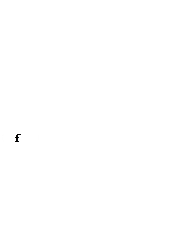
1. На первом этаме анализа схемы представленной на рис. 26 можно выделить только последовательности. Каждую выделенную последовательность  заменяем  новыми функциональными узлами: N₁, N₂, N₃, N₄ (рис. 28). В результате получаем  новую схему рис. 27.

  

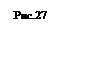
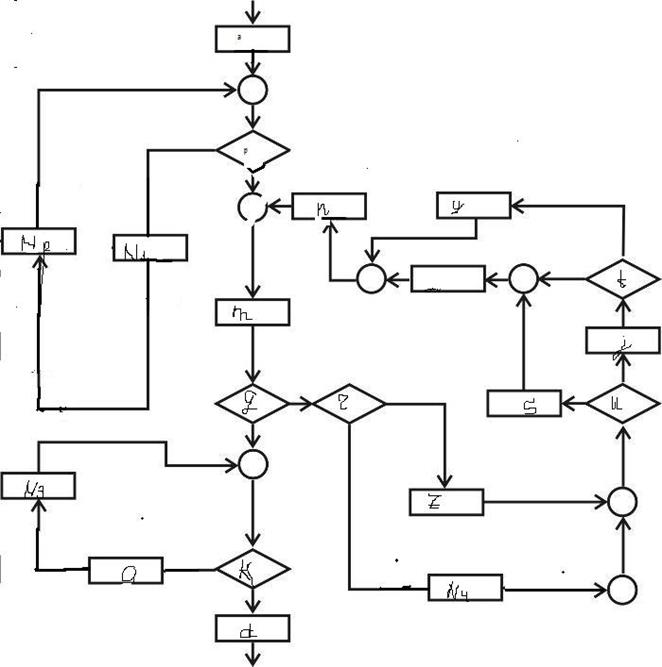
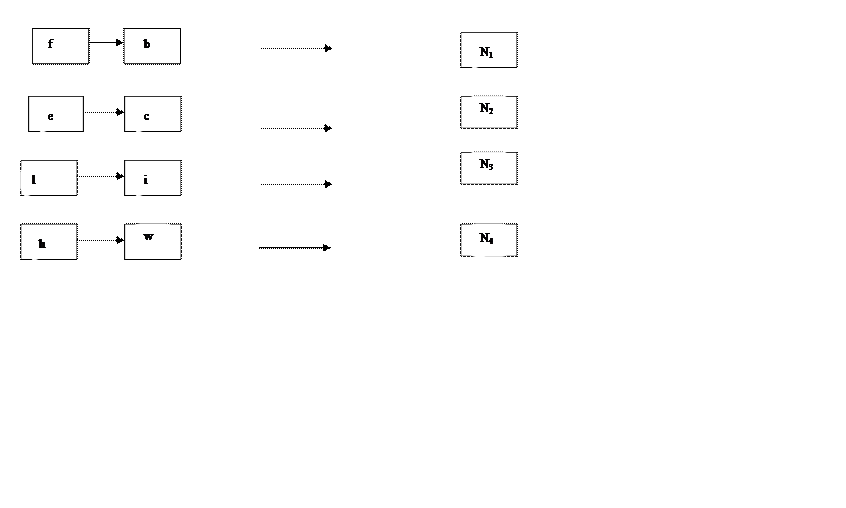
Рис. 28

2. На втором этапе  анализа выделим следующие элементарные подпрограммы и так же заменим их  новыми функциональными узлами N₅ ,N₆, N₇:

 

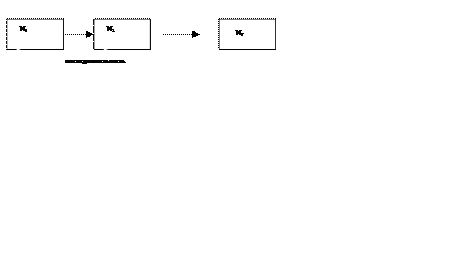
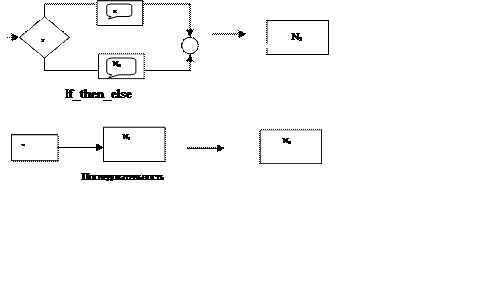
Рис. 29

Получим схему рис. 30.

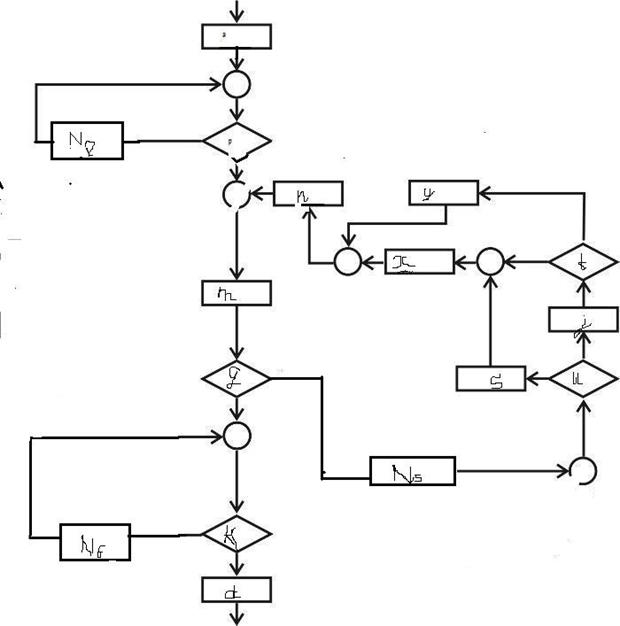
Рис. 30

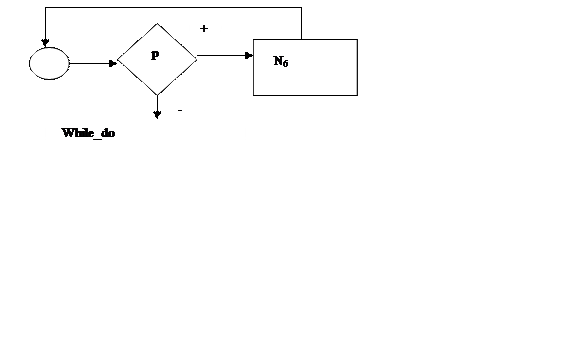
3. Объединим третий и четвёртый этапы анализа, выделив на третьем этапе две подпрограммы типа while_do,и заменяем их на функциональные блоки N₈ и N₉. ми N₈ ; d и a ; N₉, заменяем на функциональный блок N₁₀ и N₁₁ соответственно.

 

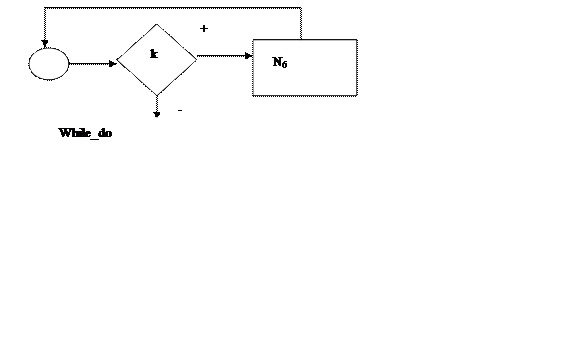
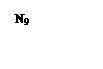
 На четвёртом этапе, выделев, получившиеся последовательности из блоков с метками N₈; d, и a; N₉,  заменим функциональными узлами N₁₀  и N₁₁ соответственно и получим схему рис. 31.

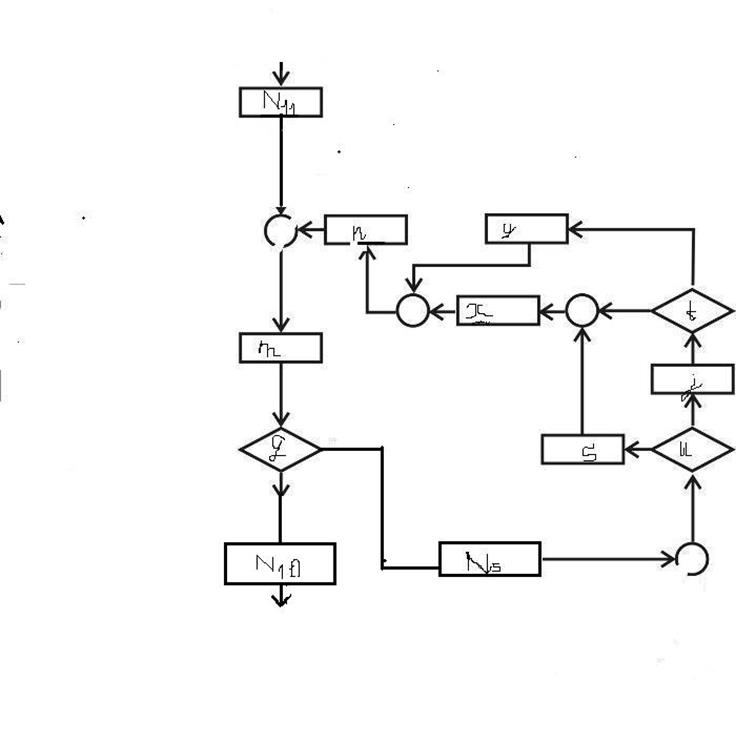
В результате получили схему, в которой нельзя выделить ни одной элементарной подпрограммы. Полученная схема называется непоименованный блок. Этот блок уже структурируется по теореме, как показано выше.

4. Правильность структурированных программ

4.1. Верификация структурированных программ

Правильность программы определяется как соответствие между программой и её заданной функцией. Корректные взаимосвязи элементов программы чрезвычайно важны, во - первых, во время чтения программы, когда необходима  правильная её интерпретация, во - вторых, когда при разработки программы стремятся достичь точного написания, в - третьих, когда на этапе испытания программы устанавливают правильность выполнения ею соответствующей функции.