Работа 18. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ СПЕКТРЫ ПОГЛОЩЕНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ
Цель работы: изучение инфракрасного спектра поглощения двухатомных газов. Определение по экспериментальным данным вращательной постоянной, момента инерции, межъядерного расстояния, силовой постоянной двухатомных молекул и заселенности вращательных уровней энергии.
18.1.
Колебательно-вращательные уровни энергии
двухатомной молекулы
У молекул, в отличие от атомов, происходит не только
движение электронов в оболочке, но и колебания ядер и вращение молекулы как
целого. Тот факт, что ядра в несколько
тысяч раз тяжелее электронов, дает возможность проводить квантовомеханические
расчеты свойств молекул на основе так называемого адиабатического
приближения. В рамках этого приближения
вводятся понятия электронного, колебательного и вращательного состояний
молекулы, а ее полная энергия Eпредставляется в виде суммы электронной ![]() , колебательной
, колебательной ![]() и
вращательной
и
вращательной ![]() энергий:
энергий:
![]() .
(18.1)
.
(18.1)
Все три вида энергии квантуются; число nнумерует электронные уровни, число u – колебательные, J – вращательные. Интервал энергий между последовательными электронными уровнями, как правило, составляет 1–10 эВ, колебательными – 10–2–10–1 эВ, вращательными – 10–4–10–3 эВ. В результате, для каждого электронного состояния молекулы получается свой набор колебательных уровней энергии, а для каждого электронно-колебательного – набор вращательных (рис.18.1).
Колебательные уровни энергии двухатомной молекулы с приемлемой точностью описываются выражением
![]() , u =
0, 1, 2,... (18.2)
, u =
0, 1, 2,... (18.2)
а вращательные –
![]() , J = 0, 1, 2,... (18.3)
, J = 0, 1, 2,... (18.3)
где
![]() – частота колебаний ядер, χ – коэффициент
ангармоничности,
– частота колебаний ядер, χ – коэффициент
ангармоничности, ![]() – вращательная постоянная. Таким образом, находящаяся в определенном
электронном состоянии двухатомная молекула может иметь ту или иную
колебательную энергию из набора (18.2) с вращательными добавками из (18.3).
– вращательная постоянная. Таким образом, находящаяся в определенном
электронном состоянии двухатомная молекула может иметь ту или иную
колебательную энергию из набора (18.2) с вращательными добавками из (18.3).

Рис. 18.1. Уровни энергии двухатомной молекулы
Первое слагаемое в (18.2) описывает уровни энергии молекулы в гармоническом приближении, а второе – поправку на ангармоничность . Коэффициент ангармоничности , χ для двухатомных молекул достаточно мал (χ <<1).
Формулы (18.2) и (18.3) выводятся квантовомеханически.
Тем не менее, параметрам ![]() , χ и
, χ и ![]() полезно
дать наглядную, классическую интерпретацию. Так, параметр
полезно
дать наглядную, классическую интерпретацию. Так, параметр ![]() интерпретируют как частоту колебаний
классического гармонического осциллятора с жесткостью (силовой постоянной) f:
интерпретируют как частоту колебаний
классического гармонического осциллятора с жесткостью (силовой постоянной) f:
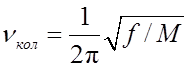 , (18.4)
, (18.4)
(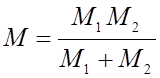 – приведенная масса молекулы, M1 и M2 – массы атомов), а коэффициент
χ – как меру отклонения колебаний от гармонических. Значения
– приведенная масса молекулы, M1 и M2 – массы атомов), а коэффициент
χ – как меру отклонения колебаний от гармонических. Значения ![]() и χ зависят от электронного состояния
инерции молекулы. Вращательная постоянная
и χ зависят от электронного состояния
инерции молекулы. Вращательная постоянная ![]() обратно пропорциональна моменту молекулы
обратно пропорциональна моменту молекулы ![]() , который может быть
выражен через приведенную массу M и среднее межъядерное расстояние
, который может быть
выражен через приведенную массу M и среднее межъядерное расстояние ![]() :
:
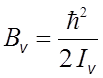 ,
, ![]() .
(18.5)
.
(18.5)
Индекс uу символов ![]() ,
,![]() и
и ![]() напоминает о том, что усредненное
межъядерное расстояние, а вместе с ним момент инерции и вращательная постоянная
зависят не только от электронного, но и от колебательного состояния молекулы. О
наборе энергий (18.3) с коэффициентом
напоминает о том, что усредненное
межъядерное расстояние, а вместе с ним момент инерции и вращательная постоянная
зависят не только от электронного, но и от колебательного состояния молекулы. О
наборе энергий (18.3) с коэффициентом ![]() , не зависящем от вращательного числа J, говорят как об уровнях жесткого ротатора.
, не зависящем от вращательного числа J, говорят как об уровнях жесткого ротатора.
Схема вращательных уровней для основного u¢¢ =0 и первого возбужденного u¢ = 1 колебательных состояний двухатомной молекулы изображена на рис. 18.3а .
18.2. Колебательно-вращательные излучательные переходы
Излучательными называют переходы как с испусканием
электромагнитного излучения, так и с его поглощением. Частота излучения ![]() при переходе определяется разностью
энергий начального и конечного состояний:
при переходе определяется разностью
энергий начального и конечного состояний:
![]() (18.6)
(18.6)
(одним штрихом принято отмечать уровень с бóльшей энергией, а двумя – с меньшей).
При колебательно-вращательных переходах электронная энергия молекулы остается постоянной, а изменяются ее колебательная и вращательная энергии. Для таких переходов
![]() . (18.7)
. (18.7)
Отметим, что только молекулы, обладающие собственным электрическим дипольным моментом имеют колебательные и вращательные спектры поглощения и испускания. Поэтому у молекул, состоящих из двух одинаковых атомов, такие спектры отсутствуют.
Если бы произошел чисто колебательный переход (J= 0' ↔ J'' = 0), то ![]() , и для двухатомной
молекулы согласно (18.2)
, и для двухатомной
молекулы согласно (18.2)
![]() . (18.8)
. (18.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.