Колебательно-вращательные спектры поглощения двухатомных молекул, страница 3

где . В этом приближении расстояние между двумя соседними линиями вращательной структуры равно , как и в чисто вращательных спектрах. При увеличении в колебательно-вращательных спектрах наблюдаются отклонения от линейных зависимостей (18.14) и (18.15), согласующиеся с формулами (18.12) и (18.13). Характер отклонений определяется знаком разности . Как правило, , поскольку асимметрия электронной кривой вызывает рост среднего межъядерного расстояния  при увеличении размаха колебаний. Таким образом,  и формулы (18.12) и (18.13) описывают соответствующее эксперименту увеличение интервалов между соседними линиями для P-ветви и сближение линий для R-ветви по мере роста  (т. е. в обоих случаях по мере отдаления от центра полосы).

18.4. Интенсивности линий вращательной структуры
        в колебательно-вращательных спектрах

Молекулы находятся в тепловом движении и при соударениях непрестанно обмениваются энергией, в результате чего осуществляется распределение молекул по энергетическим уровням. В условиях термодинамического равновесия для  N_i – среднего числа молекул на  i-том уровне – применимо распределение Больцмана:

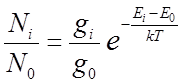                                      ,                                           (18.16)

где – число квантовых состояний молекулы с энергией  E_i (кратность вырождения, или статистический вес уровня). Если бы все состояния молекулы были невырожденными (все =1), то наиболее заселенным был бы уровень E₀ , а с ростом энергии заселенность уровней монотонно убывала.

Распределение молекул по вращательным уровням имеет более сложный характер из-за того, что вращательные состояния при J> 0 вырождены: уровню с квантовым числом J принадлежит 2 J +1 квантовое состояние. Таким образом, =2J +1  и согласно (18.16)

.

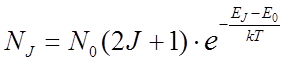Подставляя сюда E_J – E₀  из (18.3), получим явную зависимость заселенности вращательных уровней от числа  J  и температуры T

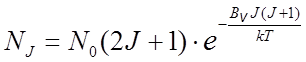                        .                             (18.17)

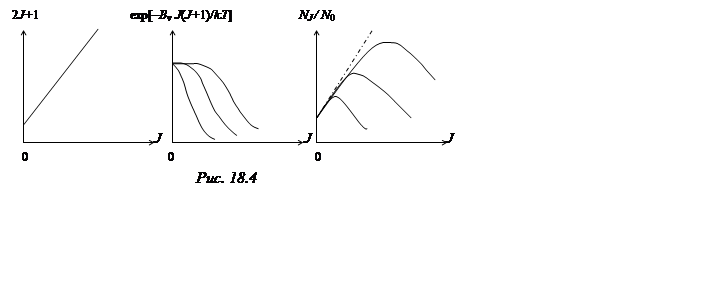
На рис. 18.4 приведены графики зависимости статистического веса , больцмановского множителя 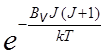 и относительной заселенности  N_J / N₀ от числа  J  для вращательных уровней молекулы СО при комнатной температуре и температурах 1000 и 2300 К.  Максимум заселенности при комнатной температуре приходится на уровень с  J=7.  С повышением температуры этот максимум смещается в сторону бóльших значений  J. Положение максимума зависит и от вращательной постоянной молекулы: чем меньше , тем при бóльших значениях  J  будет максимум заселенности.

 

Распределение молекул по вращательным уровням обусловливает распределение интенсивностей линий вращательной структуры. Оно характерно тем, что с увеличением вращательного квантового числа  J  интенсивность линий вращательной структуры в Р- и R-ветвях сначала возрастает, а потом постепенно падает (см. pис.18.2 и 18.3б). При увеличении температуры газа заселенность состояний с большими значениями  J  увеличивается и, соответственно, максимумы интенсивности в Р- и R-ветвях смещаются в разные стороны от центра полосы. При этом растет число наблюдаемых линий вращательной структуры, а интенсивность линий в максимуме падает.

Отметим, что при небольшой разрешающей силе спектральных приборов вращательная структура полос не обнаруживается, и в спектре газов наблюдаются огибающие Р- и R-ветвей.

18.5. Порядок выполнения работы и методика расчета
вращательной постоянной

Для измерения ИК спектров поглощения газа может быть использован спектрофотометр с автоматической регистрацией спектров  Specord 75 IR или любой другой аналогичный прибор, позволяющий определять волновые числа спектральных линий с точностью до 1 см^–1.

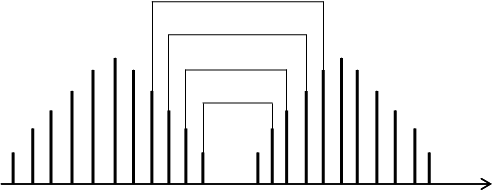
Для определения по полученным экспериментальным данным вращательной постоянной молекул рекомендуется использовать метод комбинационных разностей. Согласно этому методу измеряются комбинационные разности  – разности волновых чисел  и , для линий из R- ветви и Р-ветви с одинаковыми значениями – вращательного числа начальных (для рассматриваемых переходов с поглощением) состояний, рис. 18.5 (см. также рис. 18.3).

                 

                                , см^–1

P-ветвь                            R-ветвь

                                                                  Рис. 18.5

Чтобы связать разности  с вращательной постоянной , перейдем в формулах (18.12) и (18.13), от шкалы энергий к шкале волновых чисел. В результате:

для R-ветви –

,      J¢¢ = 0, 1, 2,… (18.18)

для Р-ветви –

,         J¢¢ =1, 2, 3… (18.19)

где .

Вычтем теперь (18.19) из (18.18):

       = 1, 2, 3…     (18.20)

Вращательную постоянную  можно найти из графика зависимости (18.20) по тангенсу угла наклона прямой    к оси абсцисс, а также по точке пересечения этой прямой с осью ординат.