Физика \ Физика атома и атомных явлений

Колебательно-вращательные спектры поглощения двухатомных молекул, страница 4

Чтобы найти вращательную постоянную , целесообразно составить комбинационные разности волновых чисел и , для линий с одинаковыми значениями – вращательного числа конечных состояний. Действительно, переходя в соотношениях (18.18) и(18.19) от J¢¢к J¢ легко получить:

для R- ветви, подставляя в (18.18) J¢¢ = J¢ –1:

J¢ = 1, 2, 3… (18.21)

а для Р-ветви, подставляя в (18.19) J¢¢ = J¢ +1:

, J¢ = 0, 1, 2,… (18.22)

Вычитая (18.22) из (18.21), получим:

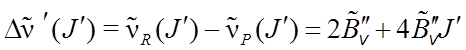, J¢ = 1, 2, 3…. (18.23)

Таким образом, вращательную постоянную можно найти из графика зависимости (18.24) как по тангенсу угла наклона прямой к оси абсцисс, так и по точке пересечения этой прямой с осью ординат.

На рис. 18.6 показано, как проводить измерения комбинационных разностей .

P-ветвь R-ветвь

Рис. 18.6.

Оценив значения вращательных постоянных и по графикам, можно перейти к их более точному определению расчетным методом. Для этого полученные экспериментальные данные следует обработать на ПК с помощью программы расчета по методу наименьших квадратов. Программа позволяет оценить и точность результатов.

18.6. Задание

1. Ознакомиться с инструкцией (Ч.1, приложение 3) по эксплуатации спектрофотометра Spесоrd 75 IR.

2. Записать спектр поглощения неизвестного двухатомного газа, выданного лаборантом, и определить волновые числа первых 10–15 линий в каждую сторону от центра полосы поглощения.

3. На полученной спектрограмме непосредственно под спектром изобразить схему колебательных и вращательных энергетических уровней и обозначить на ней наблюдаемые переходы подобно тому, как это сделано на рис. 18. 2.

4. Определить волновое число центра полосы поглощения. Используя полученное значение, а также таблицу молекулярных постоянных (табл. 18.1) двухатомных молекул, определить, какой газ находится в кювете.

5. Подсчитать приведенную массу исследуемой молекулы и с помощью (18.4) и (18.9) определить ее силовую постоянную f .

Таблица 18.1

Колебательные постоянные двухатомных молекул

в основном электронном состоянии

Молекула	, см^-1
Н₂	4400	121
Н	2323	67,5
HF	4139	90,0
HCl	2891	51,8
HBr	2649	52,2
HJ	2309	39,6
CO	2143	13,2
N₂	2358	14,1
O₂	1580	12,0
F₂	917,5	11,8
Cl₂	559,7	2,7
Br₂	325,3	1,1
J₂	214,4	0,6

6. Методом комбинационных разностей по экспериментальным данным определить постоянные и (сначала по графикам, а замем расчетным методом). По полученным значениям с помощью формул (18.5) вычислить моменты инерции и межъядерные расстояния и исследуемой молекулы.

7. По формуле (2.28) рассчитать относительную заселенность вращательных уровней для комнатной температуры. Используя полученные значения и , определить наиболее заселенный уровень.

8. Результаты расчетов сопоставить с распределением интенсивностей во вращательной структуре изученного спектра.

9. Полученные результаты представить в виде графиков и таблиц.

18.6. Контрольные вопросы

1. Какой вид имеет энергия и волновая функция молекулы в адиабатическом приближении?

2. Выведите формулу для вращательной энергии двухатомной молекулы.

3. Запишите формулу для колебательной энергии двухатомной молекулы.

4. Изобразите схему вращательных уровней двухатомной молекулы и укажите возможные переходы.

5. Изобразите схему колебательных уровней двухатомной молекулы и укажите возможные переходы.

6. Какие из перечисленных ниже молекул будут иметь вращательные и колебательные спектры поглощения и почему: H₂, O₂, Cl₂, НСl, СО?

7. Что представляет собой колебательно-вращательный спектр поглощения двухатомной молекулы? Объясните его структуру.

8. В чем суть метода комбинационных разностей для определения вращательных постоянных?

9. Как определять из экспериментальных результатов межъядерное расстояние, момент инерции молекулы и ее силовую постоянную?

10. Нарисуйте оптическую схему спектрофотометра. В чем состоит принцип работы этого прибора?

11. Из каких материалов изготовлены оптические элементы используемого спектрофотометра и почему?

1 2 3 4

Скачать файл