МАГНИТНЫЙ МОМЕНТ АТОМА. АТОМ В МАГНИТНОМ ПОЛЕ
Цели занятия: научиться вычислять магнитный момент атома и его возможные проекции с использованием правил квантования названных физических величин; научиться определять кратность вырождения состояний по магнитному квантовому числу и кратность расщепления спектральных термов атомов, обусловленного действием внешнего магнитного поля; выяснить условия реализации простого и сложного эффекта Зеемана, научиться практическому расчету величины расщепления энергетических уровней и величины смещения спектральных компонентов в условиях реализации эффекта Зеемана.
Полный орбитальный момент атома
![]() ,
,
где ![]() -
полное орбитальное квантовое число.
-
полное орбитальное квантовое число.
Полный спиновой момент атома
![]() ,
,
где S – полное спиновое квантовое число.
Полный момент импульса атома
![]() ,
,
где J – полное внутреннее квантовое число.
Магнитный момент атома
![]() ,
,
где g – множитель (фактор) Ланде:
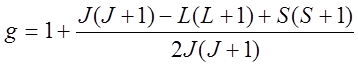 .
.
Проекция магнитного момента атома на направление внешнего магнитного поля, совпадающего по направлению с осью Z,
![]() ,
,
где ![]() -
полное магнитное квантовое число;
-
полное магнитное квантовое число; ![]() .
.
Сила, действующая на электрон в неоднородном магнитном поле,
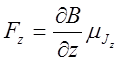 ,
,
где ![]() -
градиент магнитной индукции.
-
градиент магнитной индукции.
Частота ларморовой прецессии
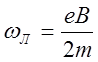 ,
,
где m – масса электрона.
Энергия атома в магнитном поле
![]() .
.
Величина расщепления спектральной линии при эффекте Зеемана:
а) сложном (аномальном)
![]() ,
,
где ![]() ,
, ![]() и
и ![]() ,
, ![]() - магнитные квантовые числа и множители
Ланде соответствующих термов;
- магнитные квантовые числа и множители
Ланде соответствующих термов;
б) простом (нормальном)
![]() ,
, ![]() .
.
Правила отбора для
квантовых чисел S, L,
J и ![]() ,
, ![]() ,
, ![]() :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
Не осуществляются переходы ![]() , а при
, а при ![]() -
переходы
-
переходы ![]() .
.
Простой эффект Зеемана реализуется:
а) для синглет - синглетных переходов;
б) для переходов с участием состояний, для которых S=0 (J=L);
в) для переходов с участием состояний, для которых L=0 (J=S);
г) в сильных магнитных полях.
Сложный (аномальный) эффект Зеемана имеет место в слабых магнитных полях для всех переходов, кроме указанных в пп. а) – в).
1. Задачи для коллективного анализа и решения
1.1. Вычислите множитель Ланде для атомов с одним валентным электроном в состояниях S иP. Ответы: 2 в S-состоянии; 2/3 и 4/3 в P-состоянии.
1.2. Вычислите множитель Ланде для атомов, находящихся в синглетных состояниях. Ответ: 1.
1.3.
Определите магнитный момент ![]() для атомов, находящихся
в состоянии
для атомов, находящихся
в состоянии ![]() . Ответ выразите в магнетонах Бора
. Ответ выразите в магнетонах Бора ![]() .
Ответ:
.
Ответ: ![]() .
.
1.4. Атом
находится в состоянии ![]() . Найдите число возможных
проекций магнитного момента на направление внешнего пол и вычислите (в
магнетонах Бора) максимальную проекцию
. Найдите число возможных
проекций магнитного момента на направление внешнего пол и вычислите (в
магнетонах Бора) максимальную проекцию ![]() .
Ответ:
.
Ответ: ![]() ;
; ![]() .
.
1.5. Вычислите
частоты ларморовой прецессии магнитных моментов электронных оболочек атомов: а)
в магнитном поле Земли (B =5.10-5
Тл); б) для атомов, находящихся в состояниях ![]() ,
, ![]() .
Ответы: 4,4.106с-1; 4,4.1012 с-1.
.
Ответы: 4,4.106с-1; 4,4.1012 с-1.
1.6.
Определите возможные значения квантового числа ![]() и
изобразите на схеме расщепление энергетических уровней атома в магнитном поле
для состояний, определяемых спектральными термами:
и
изобразите на схеме расщепление энергетических уровней атома в магнитном поле
для состояний, определяемых спектральными термами: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Ответы: -1/2, ½; -3/2,-1/2, ½, 3/2; -5/2,-3/2,-1/2, ½, 3/2, 5/2; -3, -2, -1, 0, 1, 2, 3.
1.7.
Построить схему возможных энергетических переходов в слабом магнитном
поле между состояниями атома, определяемыми следующими термами: ![]() ;
; ![]() ;
; ![]() .
.
1.8.
Вычислите смещение ![]() спектральных линий при
аномальном эффекте Зеемана в случае перехода атома из состояния, определяемого
термом
спектральных линий при
аномальном эффекте Зеемана в случае перехода атома из состояния, определяемого
термом ![]() , в состояние
, в состояние ![]() . В
качестве единицы смещения принять нормальное (лоренцево) смещение
. В
качестве единицы смещения принять нормальное (лоренцево) смещение 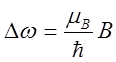 .
Ответы:
.
Ответы: 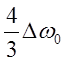 ;
; 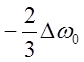 ;
; 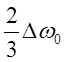 ;
; 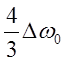 .
.
2. Задачи для самостоятельного решения
2.1. Валентный
электрон атома натрия находится в состоянии с главным квантовым числом n= 3, имея при этом максимально возможный полный
механический момент. Каков его магнитный момент в этом
состоянии? Ответ:![]() .
.
2.2. Найдите
полный механический момент атома в состоянии с S
= 3/2 и L = 2, если известно, что магнитный
момент его равен нулю. Ответ: ![]() .
.
2.3. Атом в
состоянии ![]() находится в слабом магнитном поле с
индукцией B = 1,0 кГс. Используя векторную
модель атома, найдите угловую скорость прецессии полного механического момента
этого атома.
находится в слабом магнитном поле с
индукцией B = 1,0 кГс. Используя векторную
модель атома, найдите угловую скорость прецессии полного механического момента
этого атома.
Ответ: ![]() рад/с, где
рад/с, где ![]() - множитель Ланде.
- множитель Ланде.
2.4. Какой
эффект Зеемана (простой, сложный) обнаруживают в слабом магнитном поле
спектральные линии, обусловленные следующими переходами: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ?
?
2.5.
Определите спектральный символ синглетного терма атома, если полная ширина
расщепления этого терма в слабом магнитном поле с индукцией B = 3,0 кГс составляет ![]() = 104
мкэВ.
Ответ:
= 104
мкэВ.
Ответ: ![]() .
.
2.6. Известно,
что спектральная линия ![]() = 612 нм атома обусловлена
переходом между синглетными термами. Вычислите интервал
= 612 нм атома обусловлена
переходом между синглетными термами. Вычислите интервал ![]() между
крайними компонентами этой линии в магнитном поле с индукцией
между
крайними компонентами этой линии в магнитном поле с индукцией ![]() = 10,0 кГс. Ответ:
35 пм.
= 10,0 кГс. Ответ:
35 пм.
2.7. Найдите
минимальное значение индукции магнитного поля, при котором спектральным
прибором с разрешающей способностью 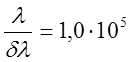 можно разрешить
компоненты спектральной линии
можно разрешить
компоненты спектральной линии ![]() = 536 нм, обусловленной
переходом между синглетными термами. Наблюдение ведут в направлении,
перпендикулярном магнитному
полю.
Ответ: 4,0 кГс = 0,40 Тл.
= 536 нм, обусловленной
переходом между синглетными термами. Наблюдение ведут в направлении,
перпендикулярном магнитному
полю.
Ответ: 4,0 кГс = 0,40 Тл.
2.8. Некоторая
спектральная линия, обусловленная переходом в ![]() -
состояние, расщепилась в слабом магнитном поле на шесть компонентов. Напишите
спектральный символ исходного
терма.
Ответ:
-
состояние, расщепилась в слабом магнитном поле на шесть компонентов. Напишите
спектральный символ исходного
терма.
Ответ: ![]() .
.
2.9. Длины
волн дублета желтой линии натрия (![]() ) равны 589,59 и 589,00
нм. Найдите: а) отношение интервалов между соседними подуровнями зеемановского
расщепления термов
) равны 589,59 и 589,00
нм. Найдите: а) отношение интервалов между соседними подуровнями зеемановского
расщепления термов ![]() и
и ![]() в
слабом магнитном поле; б) индукцию магнитного поля, при которой интервал между
соседними подуровнями зеемановского расщепления терма
в
слабом магнитном поле; б) индукцию магнитного поля, при которой интервал между
соседними подуровнями зеемановского расщепления терма ![]() будет
в 50 раз меньше естественного расщепления терма
будет
в 50 раз меньше естественного расщепления терма ![]() .
.
Ответы: 2:1; 0,55 Тл.
2.10.
Изобразите схему возможных переходов в слабом магнитном поле между термами ![]() и
и ![]() .
Вычислите для магнитного поля индукцией 4,5 кГс смещения зеемановских
компонентов этой линии (в с-1).
.
Вычислите для магнитного поля индукцией 4,5 кГс смещения зеемановских
компонентов этой линии (в с-1).
Ответ: ![]() =(
=(![]() 1,3;
1,3; ![]() 4,0;
4,0; ![]() 6,6)
6,6)![]() с-1; шесть компонентов.
с-1; шесть компонентов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.