Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Зонная пластинка. Дифракция Фраунгофера. Дифракционные решетки, страница 7

Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционной спектр), имеет вид

                                               ,

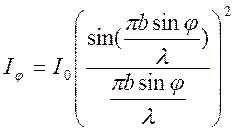      т.е.   ~  

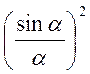
Интенсивность центрального и последующих max относятся как 1:0,047:0,017:0,0083:…, т.е. основная часть световой энергии сосредоточена в центральном max. Дифракционная картина представляет собой систему дифракционных полос, параллельных щели.

Дифракционная картина на экране существенным образом зависит от отношения b/λ (ширин щели к длине волны света). При b=mλ, sinφ=1 φ=, следовательно, сколь бы не были велики размеры линзы и экрана, на экране нельзя наблюдать max, порядок которых больше (m-1).

Шириной дифракционного max на экране Э называется расстояние между двумя ближайшими к нему дифракционными min. Например, ширина max  0-го порядка равна .

Из опыта и расчетов следует, что сужение щели ( невелико) приводит к тому, что центральный и другие max расплываются, а их яркость уменьшается. Дифракционная картинка становится мало контрастной. Кроме того, поток энергии через узкую щель крайне невелик,

так что интенсивность даже 0-го max очень мала.

Наоборот, если b/2 велико (широкая щель), то max становятся очень узкими и яркими, а число полос больше. При b>>λ центральный max представляет собой не что иное, как резкое изображение на экране источника света, образуемое линзой. Свет распространяется в соответствии с законами геометрической оптики.

Положение дифракционных max и min всех порядков зависит от длины волны λ, поэтому рассмотреный вид дифракционная картина имеет лишь для монохроматичного света. При освещении щели белым светом центральный max имеет вид белой полоски; он общий для всех длин волн (при φ=0 разность хода равна 0 для всех λ). Боковые max радужно окрашены, т.к. условие max при любых m различно для различных λ. Различно положение и min. Полное гашение света не происходит ни в одной точке экрана. Максимумы и минимумы света с различными λ перекрываются.

Максимумы 1-го, 2-го и других порядков расплывчаты и обращены фиолетовым краем к центру дифракционной картины.

Отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.

                                  § Дифракционные решетки.

Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку – систему параллельных щелей (до сотен тысяч) равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Рассматривая дифракцию Фраунгофера на одной щели, мы видели, что положение дифракционных max и min (а значит распределение интенсивности), определяется только направлением дифрагированных лучей, но не зависит от положения щели. Это означает, что перемещение щели параллельно сомой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.

Если бы щели освещались некогерентным светом, то происходило бы сложение интенсивности, т.е. интенсивностей каждой точки увеличилась бы в N раз, где N – число щелей.

Т.к. освещение решетки когерентное, то дифракционная картина определяется как результат взаимной интерференции волн, идущих от всех щелей. Т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифракцированных пучков света, идущих от всех щелей, что приводит к более сложному распределению интенсивности на экране.

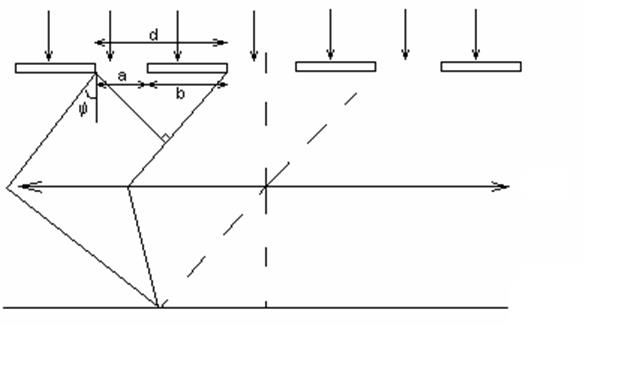Рассмотрим дифракционную решетку, на которую нормально падает плоская монохроматическая волна. Если ширина каждой щели равно a, а ширина непрозрачных участков между щелями b, то величина d=a+b называется постоянной (периодом) дифракционной решетки.

Колебания во всех точках щелей происходят в одной фазе, т.к. эти точки находятся на одной и той же волновой поверхности.

Так как щели находятся друг от друга на одинаковых расстояниях, то разность хода лучей, идущих от двух соответствующих точек соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки:

                                    ,  φ – угол дифракции.