Дифракцию плоских световых волн, или, как часто говорят, дифракцию в параллельных лучах, рассмотрел в 1821-22 г. немецкий физик И.Фраунгофер (1787-1826). Дифракционные явления Фраунгофера имеют в оптике значительно большее практическое значение, чем дифракционные явления Френеля. Дифракция Фраунгофера, как уже отмечалось, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызывающего дифракцию. Чтобы этот тип дифракции осуществить практически, точечный источник света помещают в фокус собирающей линзы, дающей параллельный пучок света, который падает затем на препятствие (отверстие или непрозрачный экран). Распределение по различным направлениям интенсивности света за препятствием исследуется с помощью второй собирающей линзы и экрана, расположенного в ее фокальной плоскости. При визуальном наблюдении вместо линзы и экрана пользуются зрительной трубой, настроенной на бесконечность.
Простейшим для расчета и практически очень важным случаем является дифракция Фраунгофера на бесконечно длинной узкой щели в непрозрачном экране (щель на практике бесконечно длинна, если ее длина значительно больше ширины).
Пусть плоская монохроматичная световая волна падает нормально плоскости узкой щели шириной b. Световое поле за щелью найдется по принципу Гюйгенса-Френеля как результат интерференции когерентных вторичных волн, исходящих от различных участков волнового фронта на щели. Вторичные источники колеблются в одной фазе, т.к. плоскость щели совпадает с фронтом падающей волны.
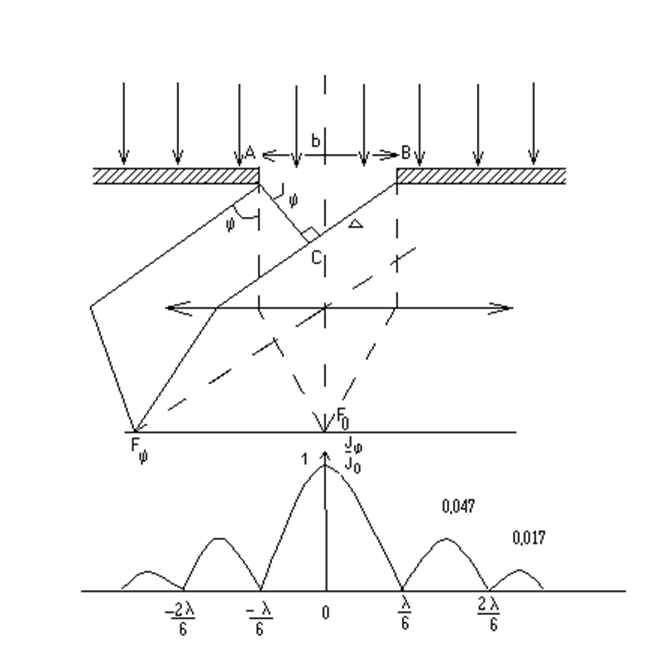 Если бы при прохождении
света через щель соблюдался закон прямолинейного распространения света, то на
экране Э, установленном в фокальной плоскости собирающей линзы, получилось бы
изображение источника света. Вследствие дифракции на узкой щели картина
коренным образом изменяется: наблюдается система дифракционных max – размытых изображений источников света, разделенных
темными промежутками – дифракционными min.
Если бы при прохождении
света через щель соблюдался закон прямолинейного распространения света, то на
экране Э, установленном в фокальной плоскости собирающей линзы, получилось бы
изображение источника света. Вследствие дифракции на узкой щели картина
коренным образом изменяется: наблюдается система дифракционных max – размытых изображений источников света, разделенных
темными промежутками – дифракционными min.
В побочном
фокусе линзы ![]() собираются все параллельные лучи, падающие
на линзу под углом φ к ее оптической оси, перпендикулярной к фронту падающей
волны.
собираются все параллельные лучи, падающие
на линзу под углом φ к ее оптической оси, перпендикулярной к фронту падающей
волны.
Оптические пути AFφ и CFφ таутохронны,
оптическая разность хода между крайними лучами, идущими от щели в
этом направлении φ: ∆=bsinφ, т.к. показатель преломления
воздуха n![]() 1.
1.
Разобьем
открытую часть волнового фронта на зоны Френеля, имеющие вид полос,
параллельных краям щели. Ширина каждой из зоны выбирается так, чтобы разность
хода от краев каждой зоны была равна λ/2. Всего на ширине
щели уместится ![]() зон.
зон.
Все зоны в заданном направлении излучают свет совершенно одинаково. Колебания вторичных источников синфазны. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.
Из приведенного
построения следует, что при интерференции света от каждой пары соседних зон
Френеля амплитуда результирующего колебания равна нулю, т.к. колебания от
каждой пары соседних зон имеют одинаковые амплитуду и противоположные фазы
(т.к. ∆= λ/2) и взаимно погашают друг друга. Таким
образом, результат интерференции света в точке ![]() определяется
тем, сколько зон Френеля для этого направления укладывается в щели.
определяется
тем, сколько зон Френеля для этого направления укладывается в щели.
Если число зон Френеля четное:
bsinφ=2m![]() (m=0,
(m=0,![]() ),
),
то в точке ![]() наблюдается дифракционный минимум (полная
темнота). Знак ‘-‘ в правой части соответствует лучам, распространяющимся от
щели под углом –φ и образующим min в точке, симметричной
наблюдается дифракционный минимум (полная
темнота). Знак ‘-‘ в правой части соответствует лучам, распространяющимся от
щели под углом –φ и образующим min в точке, симметричной ![]() относительно
главного фокуса
относительно
главного фокуса ![]() .
.
Если число зон Френеля нечетное:
bsinφ=(2m+1)
![]() (m=0,
(m=0,![]() ),
),
то в точке ![]() наблюдается дифракционный max, соответствующий действию одной нескомпенсированной зоны
Френеля. Величина m называется порядком дифракционного
максимума.
наблюдается дифракционный max, соответствующий действию одной нескомпенсированной зоны
Френеля. Величина m называется порядком дифракционного
максимума.
В направлении φ=0 щель дайствует как одна зона Френеля, т.к. колебания,
вызываемые в точке F0 всеми участками щели,
совершаются в одной фазе, в этом направлении свет распространяется с наибольшей
интенсивностью. В точке ![]() наблюдается самый
интенсивный центральный дифракционный максимум нулевого порядка.
наблюдается самый
интенсивный центральный дифракционный максимум нулевого порядка.
Рассмотренный расчет дифракционной картины, основанный на использовании метода зон Френеля, является приближенным, т.к. А зависит от φ. Точное условие min то же, а max имеет вид.
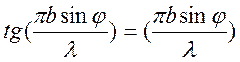
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.