Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Зонная пластинка. Дифракция Фраунгофера. Дифракционные решетки, страница 3

Найдем в произвольной точке P амплитуду световой волны, распространяющейся в однородной среде из точечного источника  S. Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей от S (поверхность сферы с центром S, радиус а которой меньше расстояния SP на величину b>>. - длина волны света).

Искомая амплитуда A зависит от результата интерференции вторичных волн, излучаемых всеми участками dФ поверхности Ф. Непосредственное решение этой задачи достаточно сложно, т.к. амплитуды и начальные фазы вторичных волн зависят от расположения соответствующих им источников dФ по отношению к точке P.

Френель предложил разбить волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до P отличались на ,т.е.

          

Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке P сферы радиусами b+, b+2, b+3, .., b+4.

Очевидно, что колебания, возбужденные в точке P соседними зонами, противоположны по фазе, так как оптическая разность хода от этих зон до точки P равна . Поэтому при наложении эти колебания будут взаимно ослаблять друг друга. Амплитуда результирующего светового колебания в точке P:

                                                                                      (*)

 где  - амплитуды колебаний, возбужденных 1-ой, 2-ой,…, m-ой зонами.

Величина  зависит от площади σ_m m-ой зоны и угла α между внешней  нормалью к поверхности зоны в какой-либо ее точке и прямой, направленной из этой точки в точку P.

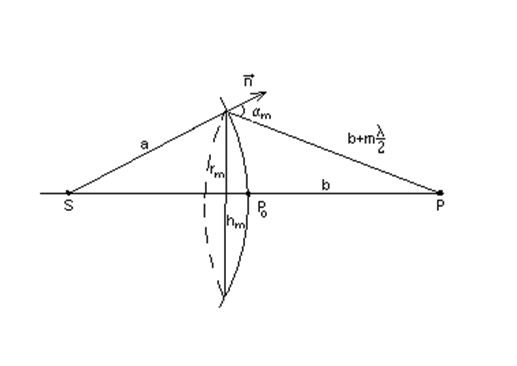Для оценки амплитуд колебания найдем площади зон Френеля. Внешняя граница m-ой зоны выделяет на волновой поверхности сферический (шаровой) сегмент высоты . Обозначив площадь этого сегмента через , найдем, что площадь m-ой зоны Френеля равна σ=, где  - площадь сферического сегмента, выделенного внешней границей m-1 – ой зоны. Из рисунка:

        

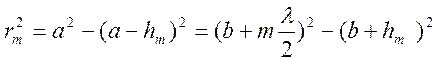
После несложных преобразований, учитывая, что λ<<a, λ<<b, получим для не очень больших m:      

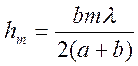                  и          .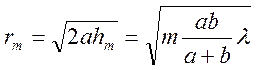

  Площадь сферического сегмента     ,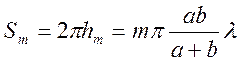

  а площадь m-ой зоны Френеля σ=

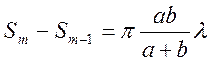
Величина σ_m не зависит от m, следовательно, при не слишком больших m площади зон Френеля одинаковы. Таким образом, построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны.

В тоже время с увеличением номера зоны возрастает угол α_m между нормалью к поверхности зоны и направлением на P. Согласно же принципу Гюйгенса-Френеля действие отдельных зон в точке P тем меньше, чем больше α. Т.е. действие зон в P постепенно убывает от центральной (около P) к периферийным (до нуля).

Кроме того, интенсивность излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от зоны до P. Учитывая оба фактора, можно записать

           

Общее число N зон Френеля, вмещающихся на части сферы, обращенной к точке P, очень велико. Например, при a=b=0,1м и λ=0,5мкм

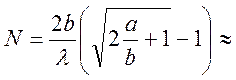          3∙

Поэтому можно считать, что в пределах не слишком больших изменений m зависимость  от m является линейной, или амплитуда колебания  от некоторой зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

           

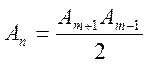
Тогда выражение (*) можно записать

           ,

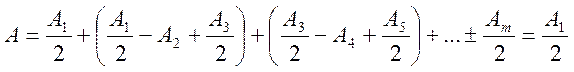т.к. выражения, стоящие в скобках, согласно ( ), равны 0, а оставшаяся часть от амплитуды последней зоны 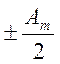 ничтожно мала.

Таким образом выражение ( ) показывает, что результирующее действие в тоске P полностью открытого фронта световых волн, возбуждаемых источником S (сферической волновой поверхностью), равно половине действия одной только центральной зоны Френеля.

Следовательно, действие всей волновой поверхности сводится к действию ее малого участка, меньшего центральной зоны.

Т.к. при не слишком больших m 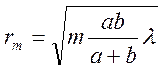, то при a=b=0,1м и λ=0,5мкм радиус первой (центральной)  зоны мм.

Таким образом, распространение света в свободном пространстве от S к P происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SP, т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет в рамках волновой теории объяснить прямолинейное распространение света в однородной среде.