Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Зонная пластинка. Дифракция Фраунгофера. Дифракционные решетки, страница 4

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используют зонные пластинки – в простейшем случае стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения зон Френеля, т.е. с радиусом  зон Френеля, определяемыми выражением ( ) для определенных значений a, b, λ. Непрозрачное покрытие наносят таким образом, что оно закрывает либо все четные, либо все нечетные зоны Френеля. Если поместить пластинку на расстоянии a от точечного источника и на расстоянии b от точки наблюдения на линии, соединяющей эти две точки, то для света данной волны λ она перекроет, например, четные зоны и оставит свободными нечетные, начиная с центральной. Результатирующая амплитуда в точке P должна быть больше, чем при полностью открытом фронте.

         A=A₁ +A₃ +A₅ +…                                      

Если общее число зон, вмещающих на пластинке, равно 2k, то . Если 2k не слишком велико, то  и, следовательно, , т.е. освещенность экрана в точке P в  раз больше, чем при беспрепятственном распространении света от источника S в точку P.

Действительно, на опыте такая пластина во много раз увеличивает интенсивность света в точке P, действуя подобно собирающей линзе. С ее помощью можно, например, формировать изображение и выполнять другие операции, характерные для линзы.

       §  Дифракция Френеля на круглом отверстии и диске.

Рассмотрим дифракцию сферических волн, или дифракцию Френеля, осуществляемую в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.

1.  Круглое отверстие.

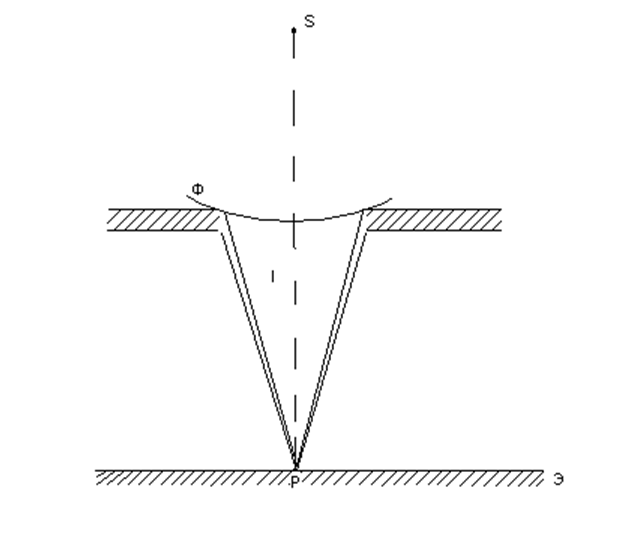Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке Р, лежащей на линии, соединяющей источник S с центром отверстия. Экран Э параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Амплитуда результирующего колебания, возбуждаемого в точке Р всеми зонами

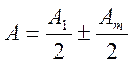                                        (из выраж. *)

  Знак ‘+’ соответствует нечетному значению m, ‘-‘ − четному.

     Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке Р будет больше, чем при свободном распространении волны (интерфереционный максимум), если четное, то амплитуда (интенсивность) будет фактически равна нулю (интерфереционный минимум). Максимум и минимум тем сильнее отличаются друг от друга, чем ближе  к .

Если в отверстие укладывается одна центральная зона Френеля, то в точке Р амплитуда  , т.е. вдвое больше, чем в отсутствии непрозрачного экрана с отверстием. Интенсивность света больше, соответственно, в 4 раза. Если в отверстие укладывается 2 зоны Френеля, то их действия в точке Р практически уничтожат друг друга из-за интерференции.

Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, т.к. соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Из соображений симметрии и из закона сохранения энергии очевидно, что дифракционная картина от круглого отверстия вблизи точки Р будет иметь вид чередующихся темных и светлых колец с центром в точке Р (m-четное − в центре темное кольцо;m-нечетное − светлое). При этом интенсивность max убывает с расстоянием от центра картины. Если отверстие освещается не монохроматическим, а белым светом, то кольца будут иметь многоцветную (радужную) окраску, т.к. число зон Френеля, укладывающихся в отверстие, зависит от λ.

При неизменном положении источника света число зон Френеля, укладывающихся в отвести, зависит от его диаметра и расстояния b. Следовательно, при изменении диаметра отверстия или при удалении от него или приближении к нему экрана Э результатирующая амплитуда в точке Р изменяется. Если диаметр отверстия велик, так что , то 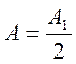, т.е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствии круглого отверстия, прямолинейно.