Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Зонная пластинка. Дифракция Фраунгофера. Дифракционные решетки, страница 5

2.  Диск.

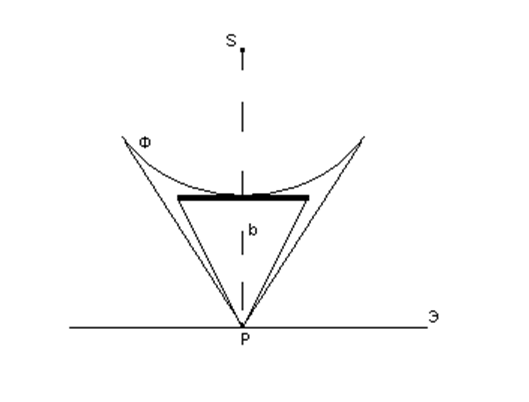Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в окрестности точки Р, лежащей на линии, соединяющей S с центром диска.

В данном случае закрытый диском участок фронта волны надо исключить из рассмотрения и зоны Френеля строить, начиная с краев диска.

Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результатирующего колебания в точке Р  равна

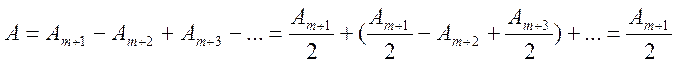
т.к. выражения в скобках равны нулю. Следовательно, в точке Р всегда наблюдается интерфереционный max, соответствующий половине действия первой открытой зоны Френеля. Экспериментально светлое пятно (пятно Пуассона) впервые получил Ораго. Как и в случае дифракции на круглом отверстии, центральный max окружен концетрическими с ним темными и светлыми кольцами, и интенсивность максимумов убывает с расстоянием от центра картины.

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки Р и, что особенно существенно, увеличивается угол α между нормалью к поверхности этой зоны и направлением на точку Р. В результате интенсивность центрального максимума с увеличением размеров диска  уменьшается. При больших размерах диска (его радиус во много раз больше радиуса закрытой им центральной зоны Френеля), за ним наблюдается обычная тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.

Дифракция на круглом отверстии и на диске впервые была рассмотрена Френелем с использованием метода Гюйгенса-Френеля и основанного на нем метода зон Френеля.

  Недостатки теории Френеля:

1.В теории Френеля предполагается, что непрозрачные части экранов не являются источниками вторичных волн а также, что амплитуды и начальные фазы колебаний в точке  поверхности Ф, не закрытых непрозрачными экранами, такие же, как и в отсутствие последних. Это неверно, т.к. граничные условия на поверхности экрана зависят от его материала. Правда, это сказывается лишь на малых, порядка λ, расстояниях от экрана. На отверстиях и экранах, размеры которых значительно больше λ, теория Френеля хорошо согласуется с опытом.

2. Теория Френеля дает неправильное значение фазы результатирующей волны. Например, при графическом сложении векторов амплитуд колебаний, возбужденных в точке Р всеми малыми элементами открытого фронта волны, оказывается, что фаза результатирующего вектора А отличается на  от  начальной фазы колебаний в точке Р, происходящих в действительности.

3. Базируется на чисто качественном постулируемом допущении о зависимости амплитуды вторичных волн от угла α.

Теория Френеля дает лишь приближенный расчетный прием. Математическое обоснование и уточнение метода Гюйгенса-Френеля было сделано в 1882 году Кирхгофом.

                             § Дифракция Фраунгофера.

Явление дифракции принято классифицировать в зависимости от расстояний источника и точки наблюдения (экрана) от препятствия, поставленного на пути распространения света. Дифракция сферических волн, картина распределения интенсивности которой наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию, называется дифракцией Френеля. Если же расстояния от препятствия до источника и точки наблюдения очень велики (бесконечно велики),  говорят о дифракции Фраунгофера.

Между френелевой и фраунгоферовой дифракциями нет принципиального различия и резкой границы. Одна непрерывно переходит в другую. Если для точки наблюдения, лежащей на оси системы, в отверстии препятствия, например, укладывается заметная часть первой зоны или несколько зон Френеля, то дифракция считается френелевой. Если в отверстии укладывается незначительная часть первой зоны Френеля, то дифракция будет фраунгоферовой.