Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Зонная пластинка. Дифракция Фраунгофера. Дифракционные решетки, страница 2

Френель вложил в принцип Гюйгенса ясный физический смысл. Предположив, что вторичные источники когерентны между собой, он дополнил принцип Гюйгенса идеей интерференции вторичных волн. Таким образом в любой точке вне вспомогательного поверхности волны, реально распространяющейся от источника, являются результатом интерференции (суперпозиции) всех когерентных вторичных волн. Выбор поверхности совершенно произволен и в каждой конкретной задаче производится таким образом, чтобы максимально упростить ее решение. Чаще всего предполагают, что поверхность совпадает в некоторый момент времени с одной из волновых поверхностей. Тогда все вторичные источники синфазны (колеблются в одной фазе).

Свет должен наблюдаться во всех местах пространства, где  при интерференции вторичные волны усиливаются; в тех же местах, где они взаимно гасят друг друга – темнота. Тем самым выясняется и физический смысл огибающей. К огибающей все вторичные волны приходят в одинаковых фазах, и их интерференция приводит к большой интенсивности света.

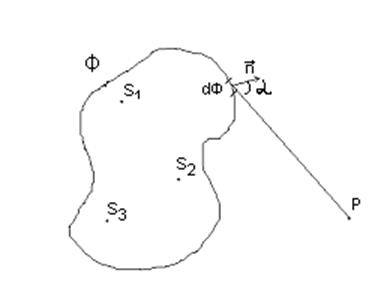
Таким образом, принцип Гюйгенса-Френеля в несколько обобщенной формулировке Рэлея (1842-1919): окружим все источники света ,,,… произвольной замкнутой поверхностью Ф. Каждую точку такой поверхности можно рассматривать как источник вторичных волн, распространяющихся во всех направлениях. Эти волны когерентны, поскольку все они возбуждаются одними и теми же первичными источниками. Световое поле, возникающее в результате их интерференции, в пространстве вне поверхности Ф совпадает с полем реальных источников света.

Эта формулировка выражает весьма общее положение. Из нее следует, что волна, отделившаяся от своих источников, в дальнейшем ведет автономное существование, совершенно не зависящее от наличия источников.

Два указанных положения недостаточны для количественного расчета дифракции света, так как ничего не говорят об интенсивности и характере направленности излучения вторичных источников.

Третье предположение Френеля: для поверхности Ф , совпадающей с волновой поверхностью, мощности вторичного излучения равных по площади участков одинаковы и пропорциональны амплитуде первичной волны. Кроме того, он считал, что каждый вторичный источник излучает свет преимущественно в направлении внешней нормали  к волновой поверхности в этой точке: амплитуда вторичных волн в направлении, составляющем с  угол α, тем менше, чем больше угол α, и равна 0 при α. Однако конкретного выражения для амплитуды вторичной волны Френель не дал (в 1883 году дал Кирхгофф). Таким образом, Френель исключил возможность возникновения “обратных вторичных волн”, распространяющихся внутрь области Ф. Качественно это можно объяснить следующими соображениями. Вторичные волны, идущие от волнового фронта вперед, вступают в свободное от возмущений пространство. Они интерферируют только друг с другом. Напротив, вторичные волны, идущие назад, вступают в пространство, где уже есть волновое возмущение. В результате интерференции обратные вторичные волны гасят прямую волну, так что после прохождения волны пространство за ней называется невозмущенным.  

 Наконец, Френель предполагал, что в том случае, когда часть поверхности Ф прикрыта непрозрачными экранами, вторичные волны излучаются только открытыми участками. Излучения их не зависят от материала, формы и размеров экранов, т.е. осуществляются так же, как если бы экранов не было.

Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т.е. определить закономерности распространения света.

В общем случае расчет интерференции вторичных волн довольно сложный и громоздкий, однако для некоторых простейших случаев нахождение амплитуды результирующего колебания осуществляется алгебраическим или геометрическим суммированием.

.

                      §2 Метод зон Френеля. Зонная пластинка.

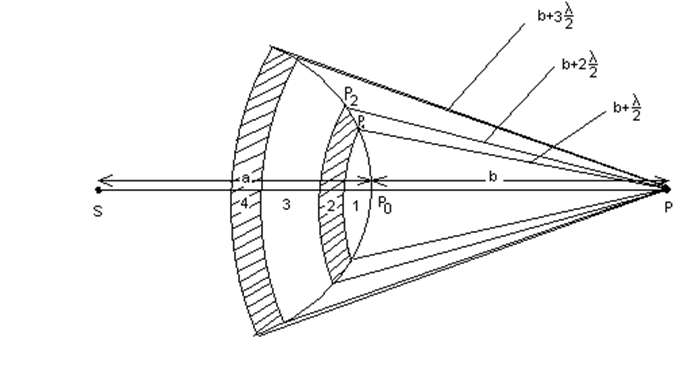Исходя из принципа Гюйгенса-Френеля, легко в рамках волновой теории ответить на вопрос о прямолинейном распространении света в свободной от препятствий однородной среде. Френель решил эту задачу, рассмотрев взаимную интерференцию вторичных волн и применив прием, получивший название метода зон Френеля.