3. ТЕОРИЯ СВЯЗАННЫХ ВИБРАТОРОВ
 ПОЛЕ ИЗЛУЧЕНИЯ
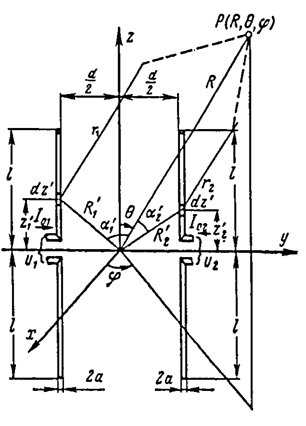
ПОЛЕ ИЗЛУЧЕНИЯРассмотрим систему из двух симметричных вибраторов, расположенных на расстоянии d друг от друга симметрично относительно оси z. Поскольку анализ производится для дальней зоны, считается, что расстояния r, r1, r2 параллельны. Считаем справочным синусоидальное распределение тока и считаем, что взаимным влиянием вибраторов можно пренебречь.
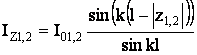 (3.1)
(3.1)
Согласно выбранной ориентации в пространстве в дальней зоне векторный потенциал имеет только z-ю составляющую.
 (3.2)
(3.2)
В данной формуле:
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
Множители являются разностями хода лучей из текущей точки интегрирования относительно начала координат.
После подстановки в ранее выведенные формулы получаем напряженность суммарного поля:
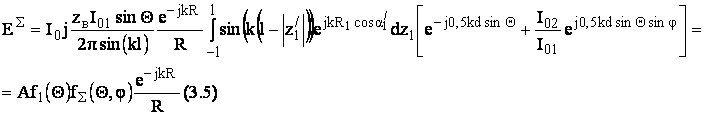
f1(Θ) – нормированная ДН одиночного вибратора (соответствующая второму интегралу).
А – амплитуда возбуждающих токов, зависит от отношения амплитуд и когерентности возбуждающих генераторов.
fΣ(Θ) – соответствующее выражение в квадратных скобках – интерференционный множитель (множитель направленности).
![]() (3.6)
(3.6)
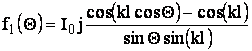 (3.7)
(3.7)
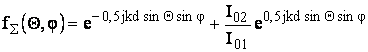 (3.8)
(3.8)
Таким образом, получение полного электромагнитного поля произвольной системы идентичных вибраторов, подчиняющейся правилу антенной решетки, достигается умножением ДН уединенного вибратора на множитель направленности.
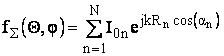 (3.7)
(3.7)
В системе из N идентичных и однонаправленных излучателей с совпадающими функциями распределения полное электромагнитное поле пропорционально произведению векторной характеристики нормированной диаграммы направленности одиночного вибратора на множитель направленности, который полностью учитывает как расположение элементов в пространстве, так и распределение комплексных амплитуд на входах.
Под принципом антенной решетки понимается, что каждый из элементов системы может быть совмещен с другим элементом с помощью только параллельного переноса (без вращения).
АНАЛИЗ ДИАГРАММЫ НАПРАВЛЕННОСТИ СИСТЕМЫ ИЗ ДВУХ ВИБРАТОРОВ
![]() (3.8)
(3.8)
Диаграмма направленности в Н-плоскости круговая, равномерная, поэтому общая диаграмма направленности будет определяться только множителем направленности.
Ф – разность фаз возбуждения вибраторов.
m – отношение комплексных амплитуд.
 (3.9)
(3.9)
После преобразований получаем следующую формулу:
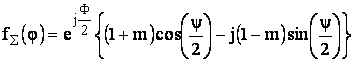 (3.10)
(3.10)
где ![]() .
.
Расположение максимумов определяется формулой:
![]() (3.11)
(3.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.