Теория связанных вибраторов, страница 2

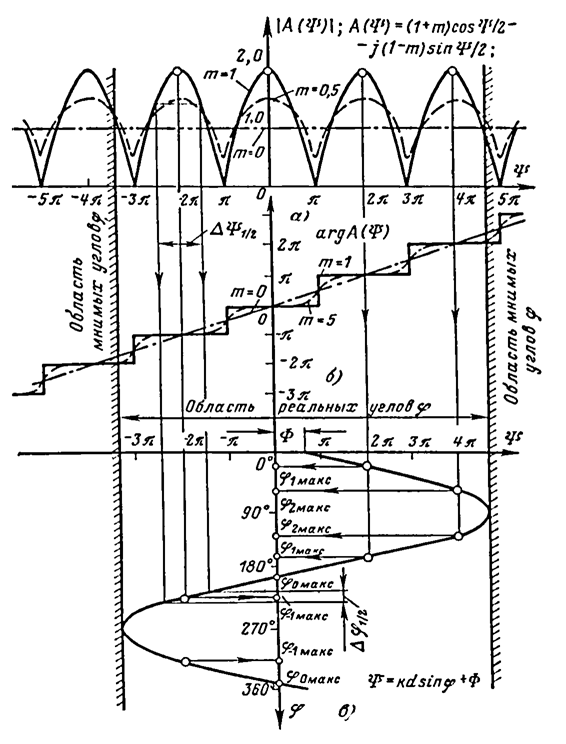
Расположение минимумов определяется формулой:

                                       (3.12)

При малых расстояниях (d<λ) диаграмма направленности имеет не более 4 лепестков. С увеличением d/λ количество лепестков увеличивается.

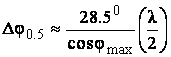;                                   (3.13)

В этом случае второй вибратор выполняет роль рефлектора относительно первого вибратора, то есть не пропускает энергию в полуплоскость за собой.

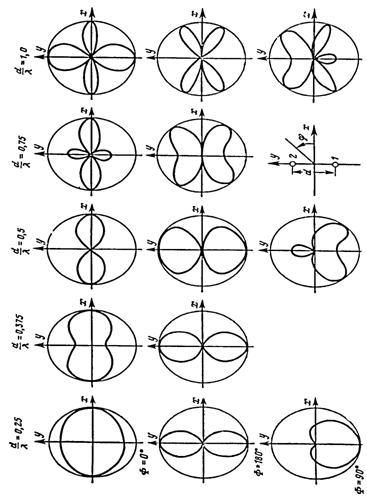
Анализ поля в Е-плоскости

В этом случае каждый из вибраторов имеет неравномерную диаграмму направленности ( в сечении приблизительно ), соответственно, в случае системы диаграмма направленности является сложной и рассчитывается методом , описанным выше.

ОСНОВНЫЕ УРАВНЕНИЯ ДЛЯ ВЗАИМНЫХ ВИБРАТОРОВ КАК
ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Воспользуемся методом наводимых ЭДС:

   - для первого вибратора;

   - для второго вибратора.                                            (3.14)

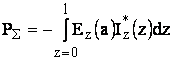                                       (3.15)

 ; “0” - на входных зажимах                   (3.16)

После подстановки и преобразований получаем следующую систему уравнений:

                                                

                                     (3.17)

где:

;

;

;

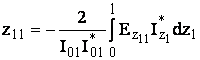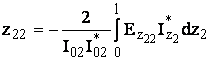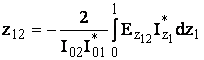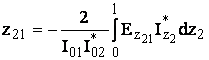                                (3.18)

Элементы z₁₁ и z₂₂ (z_ij) называются собственный импеданс вибратора. Приближенно можно считать, что это импеданс i-го вибратора при отсутствии другого (холостой ход). z₂₁ и z₁₂ – это взаимные импедансы.

z_ij = z_ji в любом случае без ферритовых элементов настройки.

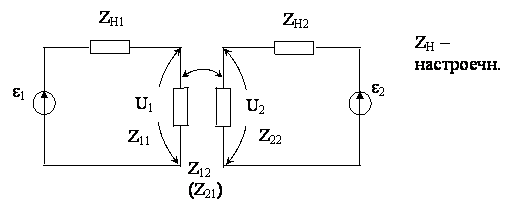В каждом конкретном случае для расчетов необходимо подставить распределение токов и зафиксировать положение в пространстве. Аналитические решения для важных случаев были получены Татариновым в 1936 г., с тех же времен – разработаны таблицы, по которым можно было производить расчеты. Целесообразно на современном этапе решать численными методами.

Для системы полуволновых вибраторов получены следующие отношения:

d = 0, z₁₂ = z₁₁ = 73.1+j42.5 (Ом).

С ростом расстояния активная часть входного импеданса напоминает поведение функции Бесселя нулевого порядка, реактивная – сдвинута на ¼ периода.

С ростом расстояния модуль входного импеданса плавно убывает, а фаза изменяется практически линейно на каждом расстоянии, равном λ, изменяется на 360⁰.