 |
 (4.3)
(4.3)
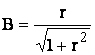 (4.4)
(4.4)
Рассмотрим поведение мгновенных значений вектора поляризации:
![]() ;
;
![]()
![]() .
. ![]() (4.5)
(4.5)
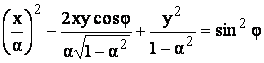 (4.6)
(4.6)
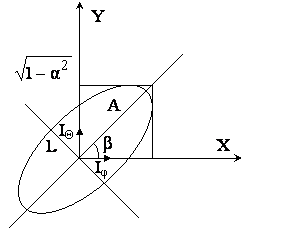
Формула (4.6) – это эллипс, полученный смещением на угол β. Поляризационный эллипс – это геометрическое место точек, которые показывают местоположение конца вектора поляризации в различные моменты времени. Таким образом, вектор поляризации совершает вращение с частотой ω, внутри эллипса поляризации направление вращения зависит от знака фазы. Если фаза положительная (φ>0), происходит вращение по часовой стрелке, если отрицательная(φ<0) – против часовой стрелки.
Частные случаи:
1. φ=0 или nπ, α=0 или α=1 – это случай линейной поляризации.
2. ![]() ,
,
![]() - круговая поляризация.
- круговая поляризация.
При задаче синтеза антенны надо знать r, β.
r – коэффициент эластичности.
![]() (4.7)
(4.7)
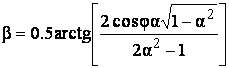 (4.8)
(4.8)
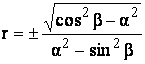 (4.9)
(4.9)
Для анализа существует обратный переход:
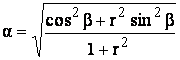 (4.10)
(4.10)
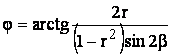 (4.11)
(4.11)
ФАЗОВАЯ ХАРАКТЕРИСТИКА НАПРАВЛЕННОСТИ
Фазовая характеристика существенно зависит от выбора начала координат, показывает изменение фазового сдвига главного компонента поляризации.
![]() (4.12)
(4.12)
Формула (4.12) – это формула эквифазной поверхности.
При Ф=const эквифазная поверхность – сфера с центром в начале координат.
Фазовый центр антенны – это точка, которая является центром эквифазной поверхности.
Для некоторых реальных антенн фазового центра не существует (рупорные, зеркальные и спиральные антенны), в этом случае может идти речь о частичном фазовом центре, то есть в каждой области углов выбирается приближение.
О фазовой характеристике можно подробнее почитать в литературе 1.
ПОЛНЫЙ КНД
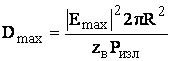 (4.13)
(4.13)
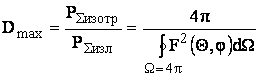 (4.14)
(4.14)
Емакс – напряженность электрического поля на расстоянии R в направлении максимума.
Ω – полный телесный угол.
Формула (4.14) – это эквивалент формулы (4.13), записанный через мощность изотропного излучателя и мощность передатчика, использующего направленную антенну, которая создает в той же точке наблюдения такое же поле, как изотропная антенна.
ИЗОТРОПНАЯ АНТЕННА
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.