Теория связанных вибраторов, страница 12

Комплексная амплитуда тока, возбуждающего n-ый элемент:

;

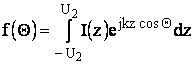                                 (6.3)

Таким образом, ДН линейной излучающей системы симметрична, обладает симметрией вращения относительно оси, в данном случае z.

От φ ДН не зависит и достаточно построить ДН в одной плоскости. Физически множитель направленности описывает интерференцию системы сферических волн, возбуждаемых отдельными элементами линейной излучающей системы.

ИДЕАЛЬНЫЙ ЛИНЕЙНЫЙ ИЗЛУЧАТЕЛЬ

,  при ;

,  при                                              (6.4)

 - коэффициент замедления, равный .

, фаза изменяется линейно. В случае, когда , получается идеальный синфазный излучатель.

Идеальный линейный излучатель (ф. 6.4) является эталонным, относительно которого в теории антенн оцениваются свойства систем излучателей. Возможны различные случаи, связанные с модулем коэффициента замедления (меньше 1 – замедленное, больше 1 – ускоренное). Знак коэффициента замедления показывает направление бегущей волны.

Подставляя (6.4) в (6.3), после преобразований получаем:

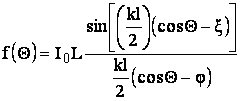                                   (6.5)

                                                         (6.6)

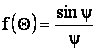                                                                (6.7)

Построение ДН в общем случае совершенно аналогично построению ДН системы вибраторных антенн. При инженерных расчетах выделяют область действительных углов ψ, после чего определяют количество лепестков ДН и расположение максимумов (подробнее – литература 1, §5.7).

ШИРИНА ЛУЧА ДН ИДЕАЛЬНОЙ ЛИНЕЙНОЙ СИСТЕМЫ

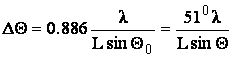                                     (6.8)

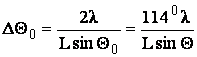                                     (6.9)

Для боковых лепестков:

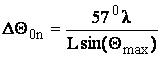                                     (6.10)

КНД  ИДЕАЛЬНОГО ЛИНЕЙНОГО ИЗЛУЧАТЕЛЯ

Оценим КПД идеального линейного излучателя, полагая, что каждый элемент системы создает изотропное излучение:

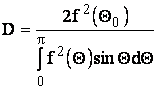                                       (6.11)

где ,   .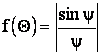

После подстановки и преобразований получаем:

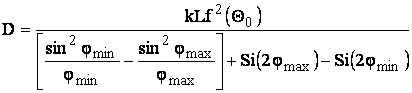,        (6.12)