Специальная теория относительности. Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского. Интервал. Собственное время. Сложение скоростей, страница 8

Условие калибровки и закон сохранения зарядов в источнике можно записать в 4 – мерной форме, используя определение дивергенции

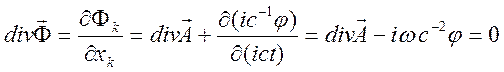                        .            (12.19)

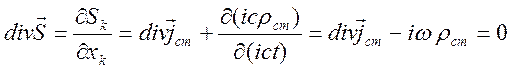                        .            (12.20)

Уравнения (12.18) – (12.20) справедливы в любой инерциальной системе отсчета. Инвариантность этих уравнений обеспечивается благодаря инвариантности трехмерных уравнений Максвелла относительно преобразования Лоренца.

Преобразование Лоренца для 4 – вектора  в случае движения системы  вдоль оси  относительно системы  имеет вид

     (12.21)

где

                                                .

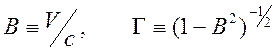Преобразование (12.21) удобно записать в матричной форме

                                                ,

где  - компоненты 4 - тензора второго ранга:

                                                .

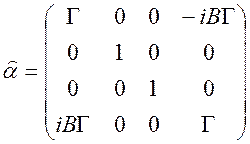Компоненты  получаются из  заменой строк на столбцы (для тензора  это делается заменой  на ). Преобразования 4 – потенциала и 4 - тока имеют вид

                                    .

            Если в системе отсчета  заряд покоится, то тока в этой системе нет, . В системе  будем иметь

                                    .

Из первого и из последнего соотношений получаем формулы преобразования плотности тока и плотности заряда

                                    .

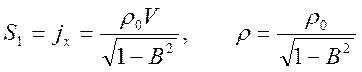С учетом последнего равенства, можно получить .

Изменение плотности заряда при переходе от к  обусловлено изменением объема . Действительно, заряд  в обеих системах одинаков, а плотность заряда определяется соотношениями

                        .

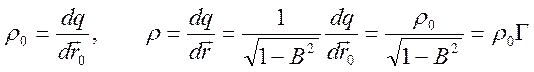Таким образом, полный заряд в заданном объеме остается неизменным

                                                .

            Вторым частным случаем является ситуация, когда в системе  имеется незаряженный проводник, по которому течет ток

                                                ,

тогда в системе  будет некоторая плотность заряда .

                        .

Эта плотность заряда определяется формулой

                                                ,             .

12.8. Тензор электромагнитного поля в вакууме. Трехмерное поле  и  связано с потенциалами

                                    .

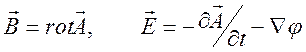Учитывая определение 4 – потенциала , получим компоненты полей

                        ,

                        ,

,

,

,

.

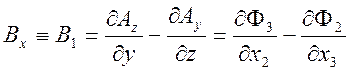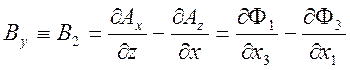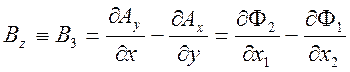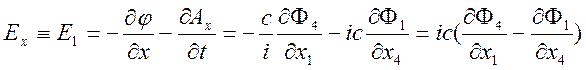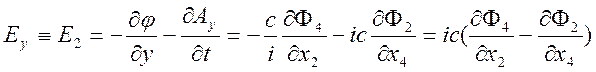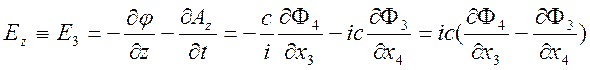Компоненты вектора  определяются по закону

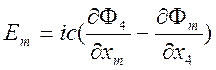
Полученные формулы представляют собой выражения для компонент поля через антисимметричный 4 – тензор второго ранга  (его называют тензором электромагнитного поля)

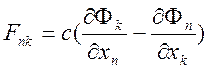                                                ,                        (12.22)

Учитывая приведенные выше соотношения, получим представление тензора в виде

                                    .

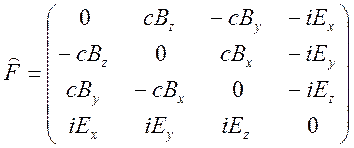Из представления (12.22) видно, что . В четырехмерном пространстве Минковского поля  и  выступают не независимо, а как составляющие единого четырехмерного электромагнитного поля, описываемые тензором . Электрическое и магнитное поля неразрывно связаны между собой. Поле от одного источника в разных инерциальных системах имеет разный вид. Если в одной инерциальной системе было только электрическое поле, то в другой инерциальной системе отсчета появится еще и магнитное поле.

12.9. Тензор индукции. Для описания поля в веществе, кроме полей и  необходимо ввести еще два вектора, например вектор электрической индукции  и вектор магнитного поля , или вектор электрической поляризации  и вектор намагничивания . Имеются  две связи между этими векторами

                                    .

Векторы  и  образуют тензор индукции  получаемый из тензора  заменой компонент  на , а компонент  на :

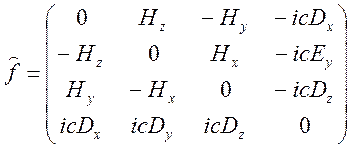                        .                     (12.22.А)

На основе тензоров  и  решается задача о преобразовании компонент поля при переходе из одной инерциальной системы в другую. Компоненты 4 – тензора  преобразуются при лоренцовском преобразовании по формуле