Специальная теория относительности. Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского. Интервал. Собственное время. Сложение скоростей, страница 7

12.6. Эффект Доплера. Аберрация света. Преобразование Лоренца может быть использовано для описания релятивистского эффекта Доплера и эффекта аберрации света (аберрация света анализировалась в разделе 12.3). Рассмотрим электромагнитное поле . Плоская монохроматическая волна имеет вид  (по – сути, обсуждаются свойства фурье - образа). Здесь частота  и волновое число  связаны между собой дисперсионным соотношением. Ограничившись распространением волны в вакууме, будем иметь представление . При преобразовании Лоренца поле  и его фурье - образ преобразуются одинаково. Фаза  стоит в показателе экспоненты, значит, она скаляр и она должна быть инвариантом. Введем в рассмотрение два 4 – вектора с компонентами  и . То, что компоненты  являются компонентами 4 – вектора (его называют волновым 4 - вектором), следует из представления , где  - скаляр,  - компоненты 4 – вектора. Значит, волновой 4 – вектор преобразуется согласно преобразованию Лоренца. 3 – вектор  преобразуется как 3 – вектор , а  - как время . Имеет место соответствие

          

Пусть инерциальная система  движется с постоянной скоростью  относительно инерциальной системы  и пусть в системе  волновой вектор и частота равны  и .

Преобразование Лоренца, соответствующие трехмерному движению системы  относительно системы  получено в разделе 12.1, и оно имеет вид

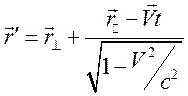                                                ,                            (12.10)

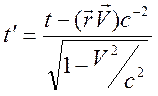                                                .                                             (12.11)

Переход к нашей задаче соответствует формальной замене . Из формул (12.10), (12.11) имеем

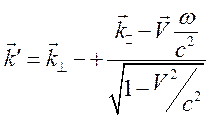                                    ,                                  (12.10.А)

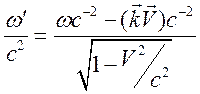                                    ,                                               (12.11.А)

где ,

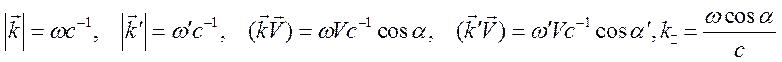 - угол между векторами  и .

Из (12.11.А) имеем описание эффекта Доплера

                                                .

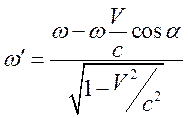Учитывая эту связь

Из (12.10.А) получим правило преобразования волновых векторов и описание аберрации света

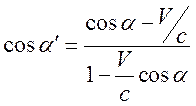                                    .                          (12.12)

Формула (12.12)описывает изменение направления распространения света в вакууме при переходе из одной инерциальной системы в другую (эффект аберрации света), а формула (12.11.А) определяет соответствующее изменение частоты – релятивистский эффект Доплера.

12.7. Преобразования Лоренца 4 – потенциала и 4 – тока в электродинамике.

Уравнения электродинамики, в отличие от уравнений классической механики, инвариантны относительно преобразования Лоренца. Для удобства преобразования полей при переходе из одной инерциальной системы в другую, целесообразно ввести понятия 4 – векторов и 4 – скаляров в четырехмерном пространстве – времени.

            В вакууме система уравнений Максвелла для гармонических полей (по – сути, речь идет о комплексных фурье - образах)

                                    ,                                              (12.13)

                                    ,                                    (12.14)

                                    ,                                                   (12.15)

                                    ,                                                 (12.16)

                                    .

Введя трехмерный векторный и скалярный потенциалы

                        ,

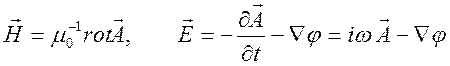уравнения (12.13) – (12.16) можно свести к уравнениям для потенциалов

                        ,                                   ,  (12.17)

где символ  означает оператор Д’Аламбера

                                    ,    

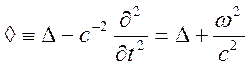и потенциалы подчинены калибровочному условию Лоренца

                                                .

Трехмерные уравнения (12.17) можно записать как одно четырехмерное уравнение для 4 – потенциала  и 4 – вектора плотности стороннего тока :

                                    .                                                               (12.18)